Menu Close

e-3x-cosxdx-help-me-please-

Tinku Tara 0 Comments
Pin




Question Number 131706 by bounhome last updated on 07/Feb/21
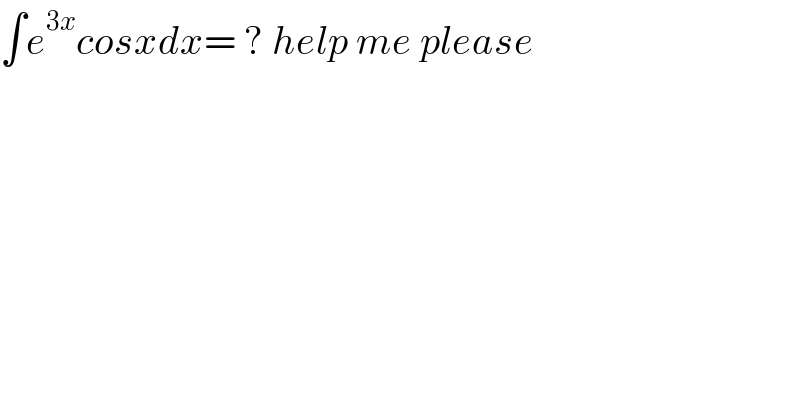
∫e^(3x) cosxdx= ? help me please
$$\int{e}^{\mathrm{3}{x}} {cosxdx}=\:?\:{help}\:{me}\:{please}\: \\ $$
Answered by mathmax by abdo last updated on 07/Feb/21
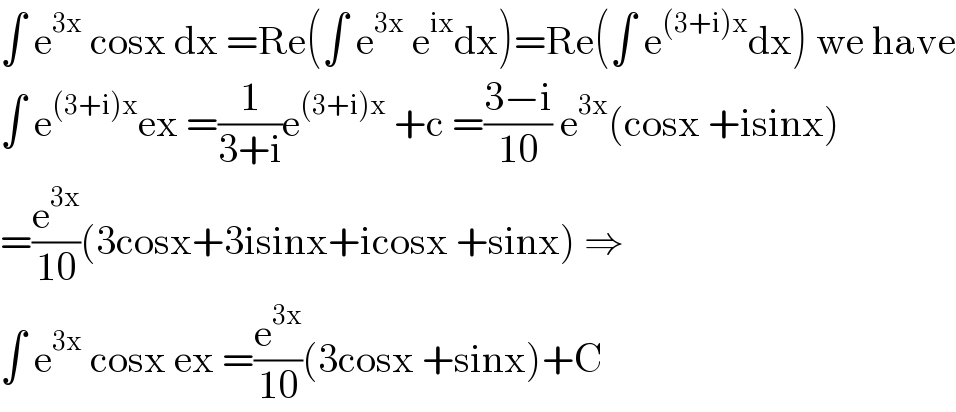
∫ e^(3x) cosx dx =Re(∫ e^(3x) e^(ix) dx)=Re(∫ e^((3+i)x) dx) we have ∫ e^((3+i)x) ex =(1/(3+i))e^((3+i)x) +c =((3−i)/(10)) e^(3x) (cosx +isinx) =(e^(3x) /(10))(3cosx+3isinx+icosx +sinx) ⇒ ∫ e^(3x) cosx ex =(e^(3x) /(10))(3cosx +sinx)+C
$$\int\:\mathrm{e}^{\mathrm{3x}} \:\mathrm{cosx}\:\mathrm{dx}\:=\mathrm{Re}\left(\int\:\mathrm{e}^{\mathrm{3x}} \:\mathrm{e}^{\mathrm{ix}} \mathrm{dx}\right)=\mathrm{Re}\left(\int\:\mathrm{e}^{\left(\mathrm{3}+\mathrm{i}\right)\mathrm{x}} \mathrm{dx}\right)\:\mathrm{we}\:\mathrm{have} \\ $$$$\int\:\mathrm{e}^{\left(\mathrm{3}+\mathrm{i}\right)\mathrm{x}} \mathrm{ex}\:=\frac{\mathrm{1}}{\mathrm{3}+\mathrm{i}}\mathrm{e}^{\left(\mathrm{3}+\mathrm{i}\right)\mathrm{x}} \:+\mathrm{c}\:=\frac{\mathrm{3}−\mathrm{i}}{\mathrm{10}}\:\mathrm{e}^{\mathrm{3x}} \left(\mathrm{cosx}\:+\mathrm{isinx}\right) \\ $$$$=\frac{\mathrm{e}^{\mathrm{3x}} }{\mathrm{10}}\left(\mathrm{3cosx}+\mathrm{3isinx}+\mathrm{icosx}\:+\mathrm{sinx}\right)\:\Rightarrow \\ $$$$\int\:\mathrm{e}^{\mathrm{3x}} \:\mathrm{cosx}\:\mathrm{ex}\:=\frac{\mathrm{e}^{\mathrm{3x}} }{\mathrm{10}}\left(\mathrm{3cosx}\:+\mathrm{sinx}\right)+\mathrm{C} \\ $$
Answered by Dwaipayan Shikari last updated on 07/Feb/21
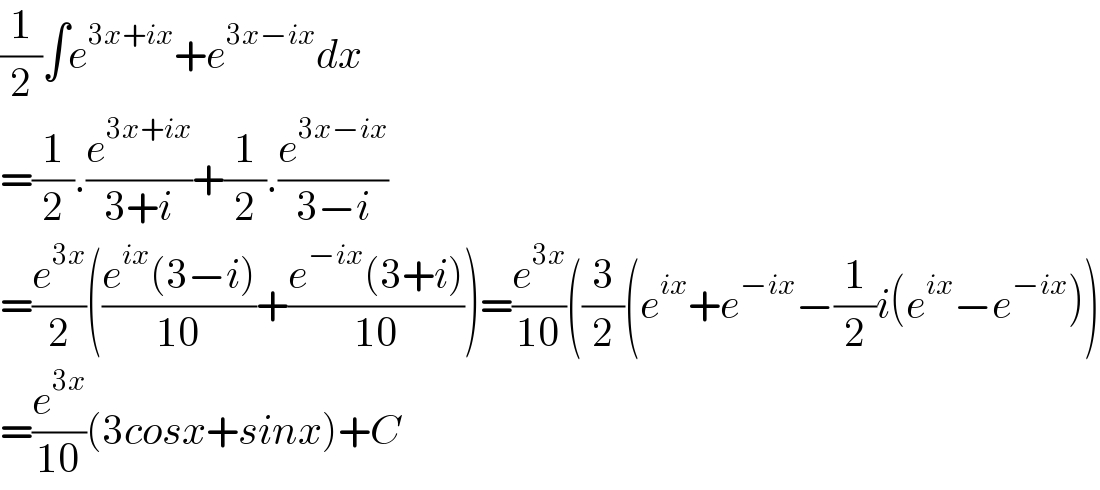
(1/2)∫e^(3x+ix) +e^(3x−ix) dx =(1/2).(e^(3x+ix) /(3+i))+(1/2).(e^(3x−ix) /(3−i)) =(e^(3x) /2)(((e^(ix) (3−i))/(10))+((e^(−ix) (3+i))/(10)))=(e^(3x) /(10))((3/2)(e^(ix) +e^(−ix) −(1/2)i(e^(ix) −e^(−ix) )) =(e^(3x) /(10))(3cosx+sinx)+C
$$\frac{\mathrm{1}}{\mathrm{2}}\int{e}^{\mathrm{3}{x}+{ix}} +{e}^{\mathrm{3}{x}−{ix}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}.\frac{{e}^{\mathrm{3}{x}+{ix}} }{\mathrm{3}+{i}}+\frac{\mathrm{1}}{\mathrm{2}}.\frac{{e}^{\mathrm{3}{x}−{ix}} }{\mathrm{3}−{i}} \\ $$$$=\frac{{e}^{\mathrm{3}{x}} }{\mathrm{2}}\left(\frac{{e}^{{ix}} \left(\mathrm{3}−{i}\right)}{\mathrm{10}}+\frac{{e}^{−{ix}} \left(\mathrm{3}+{i}\right)}{\mathrm{10}}\right)=\frac{{e}^{\mathrm{3}{x}} }{\mathrm{10}}\left(\frac{\mathrm{3}}{\mathrm{2}}\left({e}^{{ix}} +{e}^{−{ix}} −\frac{\mathrm{1}}{\mathrm{2}}{i}\left({e}^{{ix}} −{e}^{−{ix}} \right)\right)\right. \\ $$$$=\frac{{e}^{\mathrm{3}{x}} }{\mathrm{10}}\left(\mathrm{3}{cosx}+{sinx}\right)+{C} \\ $$
Answered by physicstutes last updated on 07/Feb/21
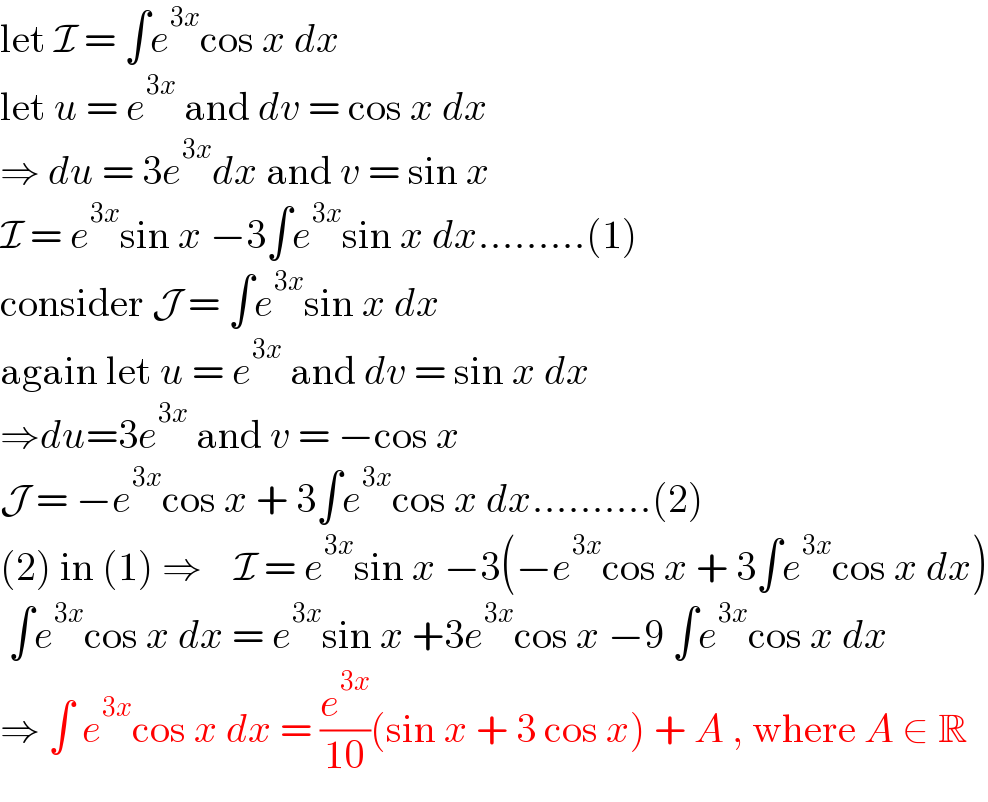
let I = ∫e^(3x) cos x dx let u = e^(3x) and dv = cos x dx ⇒ du = 3e^(3x) dx and v = sin x I = e^(3x) sin x −3∫e^(3x) sin x dx.........(1) consider J = ∫e^(3x) sin x dx again let u = e^(3x) and dv = sin x dx ⇒du=3e^(3x) and v = −cos x J = −e^(3x) cos x + 3∫e^(3x) cos x dx..........(2) (2) in (1) ⇒ I = e^(3x) sin x −3(−e^(3x) cos x + 3∫e^(3x) cos x dx) ∫e^(3x) cos x dx = e^(3x) sin x +3e^(3x) cos x −9 ∫e^(3x) cos x dx ⇒ ∫ e^(3x) cos x dx = (e^(3x) /(10))(sin x + 3 cos x) + A , where A ∈ R
$$\mathrm{let}\:\mathcal{I}\:=\:\int{e}^{\mathrm{3}{x}} \mathrm{cos}\:{x}\:{dx} \\ $$$$\mathrm{let}\:{u}\:=\:{e}^{\mathrm{3}{x}} \:\mathrm{and}\:{dv}\:=\:\mathrm{cos}\:{x}\:{dx} \\ $$$$\Rightarrow\:{du}\:=\:\mathrm{3}{e}^{\mathrm{3}{x}} {dx}\:\mathrm{and}\:{v}\:=\:\mathrm{sin}\:{x} \\ $$$$\mathcal{I}\:=\:{e}^{\mathrm{3}{x}} \mathrm{sin}\:{x}\:−\mathrm{3}\int{e}^{\mathrm{3}{x}} \mathrm{sin}\:{x}\:{dx}………\left(\mathrm{1}\right) \\ $$$$\mathrm{consider}\:\mathcal{J}\:=\:\int{e}^{\mathrm{3}{x}} \mathrm{sin}\:{x}\:{dx} \\ $$$$\mathrm{again}\:\mathrm{let}\:{u}\:=\:{e}^{\mathrm{3}{x}} \:\mathrm{and}\:{dv}\:=\:\mathrm{sin}\:{x}\:{dx} \\ $$$$\Rightarrow{du}=\mathrm{3}{e}^{\mathrm{3}{x}} \:\mathrm{and}\:{v}\:=\:−\mathrm{cos}\:{x} \\ $$$$\mathcal{J}\:=\:−{e}^{\mathrm{3}{x}} \mathrm{cos}\:{x}\:+\:\mathrm{3}\int{e}^{\mathrm{3}{x}} \mathrm{cos}\:{x}\:{dx}……….\left(\mathrm{2}\right) \\ $$$$\left(\mathrm{2}\right)\:\mathrm{in}\:\left(\mathrm{1}\right)\:\Rightarrow\:\:\:\:\mathcal{I}\:=\:{e}^{\mathrm{3}{x}} \mathrm{sin}\:{x}\:−\mathrm{3}\left(−{e}^{\mathrm{3}{x}} \mathrm{cos}\:{x}\:+\:\mathrm{3}\int{e}^{\mathrm{3}{x}} \mathrm{cos}\:{x}\:{dx}\right) \\ $$$$\:\int{e}^{\mathrm{3}{x}} \mathrm{cos}\:{x}\:{dx}\:=\:{e}^{\mathrm{3}{x}} \mathrm{sin}\:{x}\:+\mathrm{3}{e}^{\mathrm{3}{x}} \mathrm{cos}\:{x}\:−\mathrm{9}\:\int{e}^{\mathrm{3}{x}} \mathrm{cos}\:{x}\:{dx} \\ $$$$\Rightarrow\:\int\:{e}^{\mathrm{3}{x}} \mathrm{cos}\:{x}\:{dx}\:=\:\frac{{e}^{\mathrm{3}{x}} }{\mathrm{10}}\left(\mathrm{sin}\:{x}\:+\:\mathrm{3}\:\mathrm{cos}\:{x}\right)\:+\:{A}\:,\:\mathrm{where}\:{A}\:\in\:\mathbb{R} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *