Question Number 142176 by malwaan last updated on 27/May/21
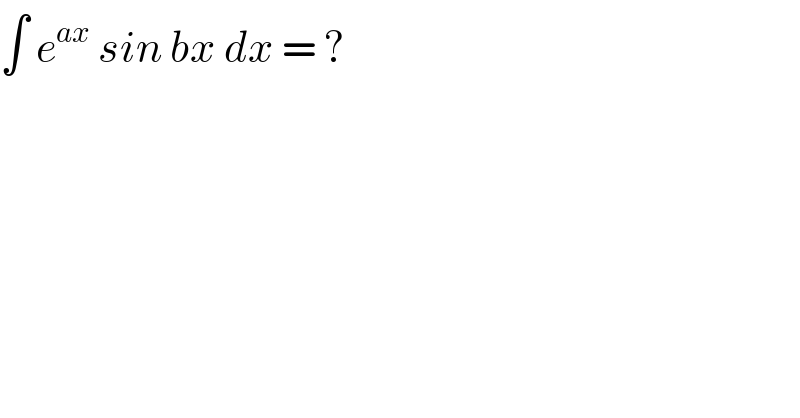
$$\int\:{e}^{{ax}} \:{sin}\:{bx}\:{dx}\:=\:? \\ $$
Answered by Dwaipayan Shikari last updated on 27/May/21

$${sin}\left({bx}\right)=\frac{{e}^{{ibx}} −{e}^{−{ibx}} }{\mathrm{2}{i}} \\ $$$$\int{e}^{{ax}} \left(\frac{{e}^{{ibx}} −{e}^{−{ibx}} }{\mathrm{2}{i}}\right){dx} \\ $$$$=\frac{{e}^{{ax}} }{\mathrm{2}{i}}\left(\frac{\mathrm{1}}{{a}+{ib}}{e}^{{ibx}} −\frac{{e}^{−{ibx}} }{{a}−{ib}}\right) \\ $$$$=\frac{{e}^{{ax}} }{\mathrm{2}{i}}\left(\frac{{a}−{ib}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{e}^{{ibx}} −\frac{{a}+{ib}}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }{e}^{−{ibx}} \right) \\ $$$$={e}^{{ax}} \left(\frac{{asin}\left({bx}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }−\frac{{bcos}\left({bx}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} }\right)+{C} \\ $$
