Question Number 6582 by Temp last updated on 04/Jul/16
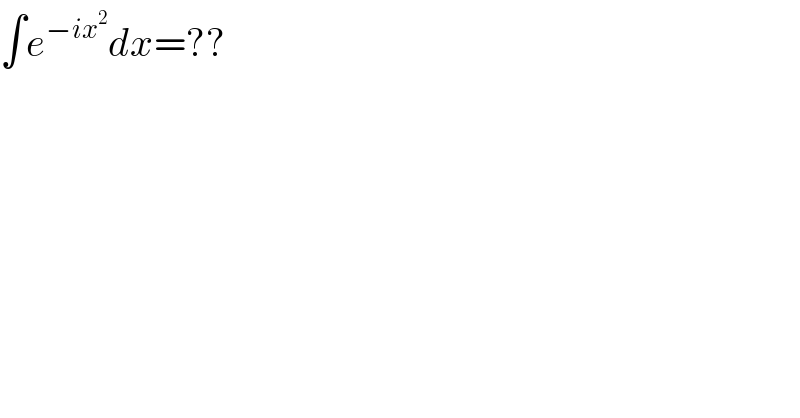
$$\int{e}^{−{ix}^{\mathrm{2}} } {dx}=?? \\ $$
Answered by Yozzii last updated on 04/Jul/16
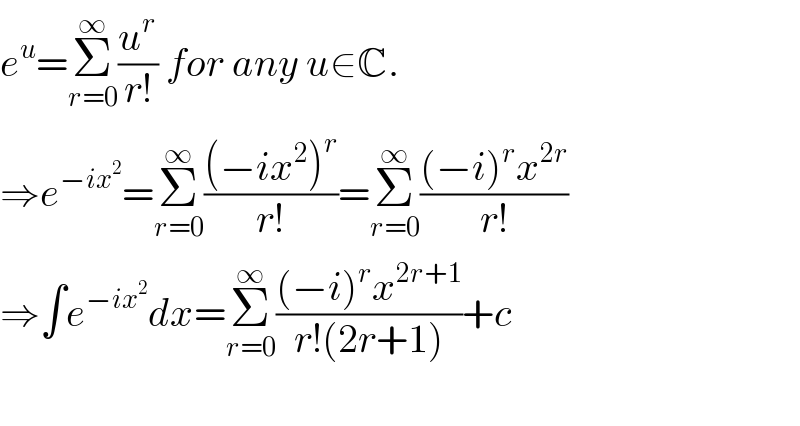
$${e}^{{u}} =\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{{u}^{{r}} }{{r}!}\:{for}\:{any}\:{u}\in\mathbb{C}. \\ $$$$\Rightarrow{e}^{−{ix}^{\mathrm{2}} } =\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{ix}^{\mathrm{2}} \right)^{{r}} }{{r}!}=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{i}\right)^{{r}} {x}^{\mathrm{2}{r}} }{{r}!} \\ $$$$\Rightarrow\int{e}^{−{ix}^{\mathrm{2}} } {dx}=\underset{{r}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\left(−{i}\right)^{{r}} {x}^{\mathrm{2}{r}+\mathrm{1}} }{{r}!\left(\mathrm{2}{r}+\mathrm{1}\right)}+{c} \\ $$$$ \\ $$
Commented by Temp last updated on 04/Jul/16
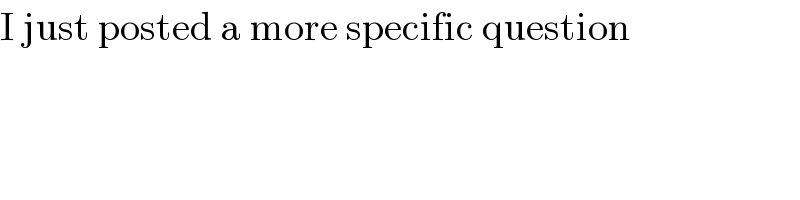
$$\mathrm{I}\:\mathrm{just}\:\mathrm{posted}\:\mathrm{a}\:\mathrm{more}\:\mathrm{specific}\:\mathrm{question} \\ $$
