Question Number 74210 by malikmasood3535@gmail.com last updated on 20/Nov/19

$$\int{e}^{{t}} \mathrm{cos}\:{e}^{{t}} {dt} \\ $$
Answered by mind is power last updated on 20/Nov/19
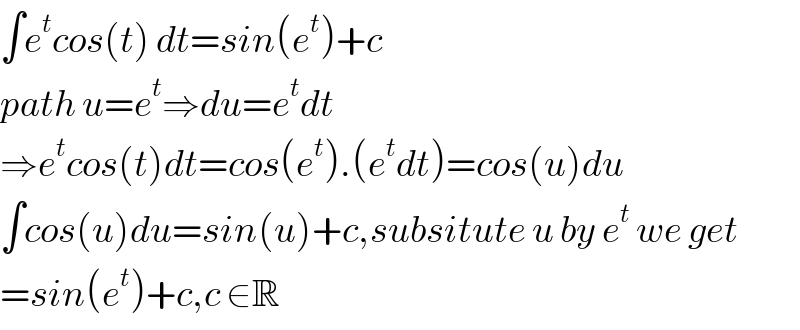
$$\int{e}^{{t}} {cos}\left({t}\right)\:{dt}={sin}\left({e}^{{t}} \right)+{c} \\ $$$${path}\:{u}={e}^{{t}} \Rightarrow{du}={e}^{{t}} {dt} \\ $$$$\Rightarrow{e}^{{t}} {cos}\left({t}\right){dt}={cos}\left({e}^{{t}} \right).\left({e}^{{t}} {dt}\right)={cos}\left({u}\right){du} \\ $$$$\int{cos}\left({u}\right){du}={sin}\left({u}\right)+{c},{subsitute}\:{u}\:{by}\:{e}^{{t}} \:{we}\:{get} \\ $$$$={sin}\left({e}^{{t}} \right)+{c},{c}\:\in\mathbb{R} \\ $$
