Question Number 142789 by daniel1301 last updated on 05/Jun/21
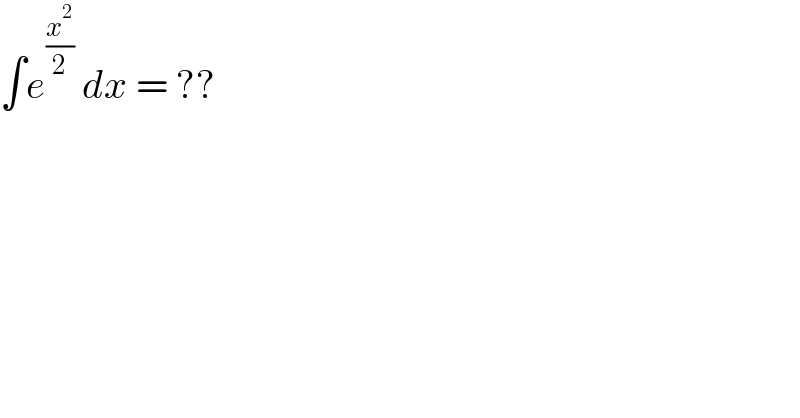
$$\int{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} \:{dx}\:=\:?? \\ $$
Answered by MJS_new last updated on 05/Jun/21
![∫e^(x^2 /2) dx= [t=(((√2)x)/( 2)) → dx=(√2)dt] =(√2)∫e^t^2 dt=(√2)×((√π)/2)∫e^t^2 ×(2/( (√π)))dt=((√(2π))/2)∫((2e^t^2 )/( (√π)))dt= =((√(2π))/2)erfi t = =((√(2π))/2)erfi (((√2)x)/2) +C (!!)](https://www.tinkutara.com/question/Q142795.png)
$$\int\mathrm{e}^{\frac{{x}^{\mathrm{2}} }{\mathrm{2}}} {dx}= \\ $$$$\:\:\:\:\:\left[{t}=\frac{\sqrt{\mathrm{2}}{x}}{\:\mathrm{2}}\:\rightarrow\:{dx}=\sqrt{\mathrm{2}}{dt}\right] \\ $$$$=\sqrt{\mathrm{2}}\int\mathrm{e}^{{t}^{\mathrm{2}} } {dt}=\sqrt{\mathrm{2}}×\frac{\sqrt{\pi}}{\mathrm{2}}\int\mathrm{e}^{{t}^{\mathrm{2}} } ×\frac{\mathrm{2}}{\:\sqrt{\pi}}{dt}=\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{2}}\int\frac{\mathrm{2e}^{{t}^{\mathrm{2}} } }{\:\sqrt{\pi}}{dt}= \\ $$$$=\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{2}}\mathrm{erfi}\:{t}\:= \\ $$$$=\frac{\sqrt{\mathrm{2}\pi}}{\mathrm{2}}\mathrm{erfi}\:\frac{\sqrt{\mathrm{2}}{x}}{\mathrm{2}}\:+{C}\:\:\:\:\:\left(!!\right) \\ $$
Commented by daniel1301 last updated on 05/Jun/21

$${beautiful}\: \\ $$
Answered by Dwaipayan Shikari last updated on 05/Jun/21
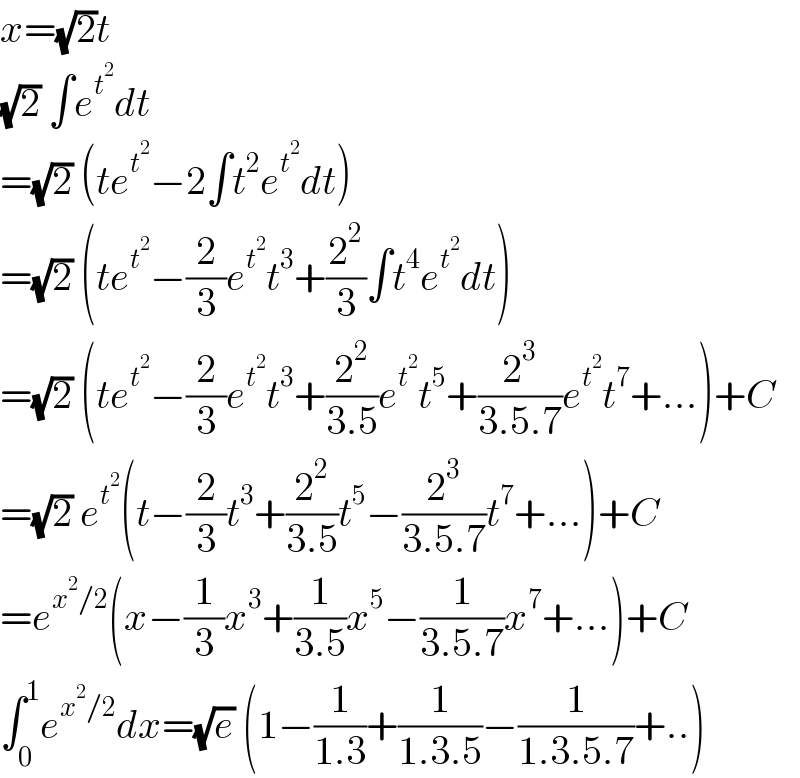
$${x}=\sqrt{\mathrm{2}}{t} \\ $$$$\sqrt{\mathrm{2}}\:\int{e}^{{t}^{\mathrm{2}} } {dt} \\ $$$$=\sqrt{\mathrm{2}}\:\left({te}^{{t}^{\mathrm{2}} } −\mathrm{2}\int{t}^{\mathrm{2}} {e}^{{t}^{\mathrm{2}} } {dt}\right) \\ $$$$=\sqrt{\mathrm{2}}\:\left({te}^{{t}^{\mathrm{2}} } −\frac{\mathrm{2}}{\mathrm{3}}{e}^{{t}^{\mathrm{2}} } {t}^{\mathrm{3}} +\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}}\int{t}^{\mathrm{4}} {e}^{{t}^{\mathrm{2}} } {dt}\right) \\ $$$$=\sqrt{\mathrm{2}}\:\left({te}^{{t}^{\mathrm{2}} } −\frac{\mathrm{2}}{\mathrm{3}}{e}^{{t}^{\mathrm{2}} } {t}^{\mathrm{3}} +\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}.\mathrm{5}}{e}^{{t}^{\mathrm{2}} } {t}^{\mathrm{5}} +\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}.\mathrm{5}.\mathrm{7}}{e}^{{t}^{\mathrm{2}} } {t}^{\mathrm{7}} +…\right)+{C} \\ $$$$=\sqrt{\mathrm{2}}\:{e}^{{t}^{\mathrm{2}} } \left({t}−\frac{\mathrm{2}}{\mathrm{3}}{t}^{\mathrm{3}} +\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{3}.\mathrm{5}}{t}^{\mathrm{5}} −\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}.\mathrm{5}.\mathrm{7}}{t}^{\mathrm{7}} +…\right)+{C} \\ $$$$={e}^{{x}^{\mathrm{2}} /\mathrm{2}} \left({x}−\frac{\mathrm{1}}{\mathrm{3}}{x}^{\mathrm{3}} +\frac{\mathrm{1}}{\mathrm{3}.\mathrm{5}}{x}^{\mathrm{5}} −\frac{\mathrm{1}}{\mathrm{3}.\mathrm{5}.\mathrm{7}}{x}^{\mathrm{7}} +…\right)+{C} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {e}^{{x}^{\mathrm{2}} /\mathrm{2}} {dx}=\sqrt{{e}}\:\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}.\mathrm{3}}+\frac{\mathrm{1}}{\mathrm{1}.\mathrm{3}.\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{1}.\mathrm{3}.\mathrm{5}.\mathrm{7}}+..\right) \\ $$
Commented by daniel1301 last updated on 05/Jun/21

$${thanks} \\ $$
