Question Number 497 by 13/NaSaNa(N)056565 last updated on 25/Jan/15

$$\int{e}^{{x}} \mathrm{sin}\:\mathrm{2}{x}\:{dx} \\ $$
Answered by prakash jain last updated on 16/Jan/15
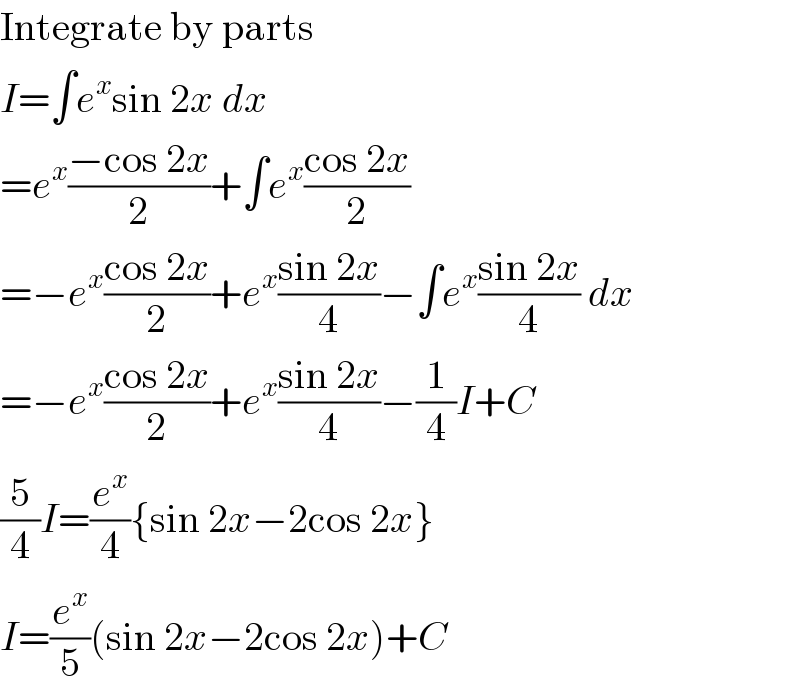
$$\mathrm{Integrate}\:\mathrm{by}\:\mathrm{parts} \\ $$$${I}=\int{e}^{{x}} \mathrm{sin}\:\mathrm{2}{x}\:{dx} \\ $$$$={e}^{{x}} \frac{−\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}+\int{e}^{{x}} \frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}} \\ $$$$=−{e}^{{x}} \frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}+{e}^{{x}} \frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{4}}−\int{e}^{{x}} \frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{4}}\:{dx} \\ $$$$=−{e}^{{x}} \frac{\mathrm{cos}\:\mathrm{2}{x}}{\mathrm{2}}+{e}^{{x}} \frac{\mathrm{sin}\:\mathrm{2}{x}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}{I}+{C} \\ $$$$\frac{\mathrm{5}}{\mathrm{4}}{I}=\frac{{e}^{{x}} }{\mathrm{4}}\left\{\mathrm{sin}\:\mathrm{2}{x}−\mathrm{2cos}\:\mathrm{2}{x}\right\} \\ $$$${I}=\frac{{e}^{{x}} }{\mathrm{5}}\left(\mathrm{sin}\:\mathrm{2}{x}−\mathrm{2cos}\:\mathrm{2}{x}\right)+{C} \\ $$
