Question Number 911 by 112358 last updated on 22/Apr/15

$${Eight}\:{people}\:{are}\:{seated}\:{around} \\ $$$${a}\:{circular}\:{table}.\:{Each}\:{person} \\ $$$${must}\:{shake}\:{everyone}'{s}\:{hand}\:{but} \\ $$$${they}\:{must}\:{not}\:{shake}\:{hands}\:{with} \\ $$$${the}\:{two}\:{persons}\:{seated}\:{at}\:{their}\:{sides}. \\ $$$${How}\:{many}\:{handshakes}\:{occur}? \\ $$
Answered by prakash jain last updated on 22/Apr/15
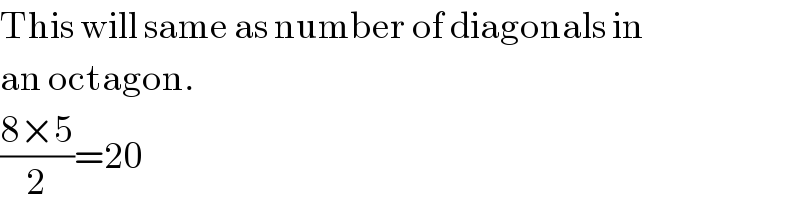
$$\mathrm{This}\:\mathrm{will}\:\mathrm{same}\:\mathrm{as}\:\mathrm{number}\:\mathrm{of}\:\mathrm{diagonals}\:\mathrm{in} \\ $$$$\mathrm{an}\:\mathrm{octagon}. \\ $$$$\frac{\mathrm{8}×\mathrm{5}}{\mathrm{2}}=\mathrm{20} \\ $$
Commented by 112358 last updated on 23/Apr/15

$${Would}\:{it}\:{be}\:{possible}\:{to}\:{generalise} \\ $$$${this}\:{problem}\:{where}\:{there}\:{are}\:\boldsymbol{{n}}\: \\ $$$${people}\:{and}\:\boldsymbol{{m}}\:{number}\:{of}\:{persons} \\ $$$${seated}\:{on}\:{both}\:{sides}\:{of}\:{each}\: \\ $$$${person}\:{with}\:{whom}\:{hands}\:{cannot} \\ $$$${be}\:{shaken}? \\ $$$$ \\ $$
Commented by prakash jain last updated on 23/Apr/15

$$\frac{{n}×\left({n}−\mathrm{2}{m}−\mathrm{1}\right)}{\mathrm{2}} \\ $$$$\mathrm{2}{m},\:{m}\:{people}\:{on}\:{either}\:{side} \\ $$$$\mathrm{1},\:{self} \\ $$$$\mathrm{So}\:\mathrm{each}\:\mathrm{point}\:\mathrm{is}\:\mathrm{connected}\:\mathrm{with}\:{n}−\left(\mathrm{2}{m}+\mathrm{1}\right) \\ $$$$\mathrm{points}. \\ $$$$\mathrm{Divide}\:\mathrm{by}\:\mathrm{2}\:\mathrm{for}\:\mathrm{counting}\:\mathrm{each}\:\mathrm{line}\:\mathrm{twice}. \\ $$
