Question Number 141274 by mnjuly1970 last updated on 17/May/21
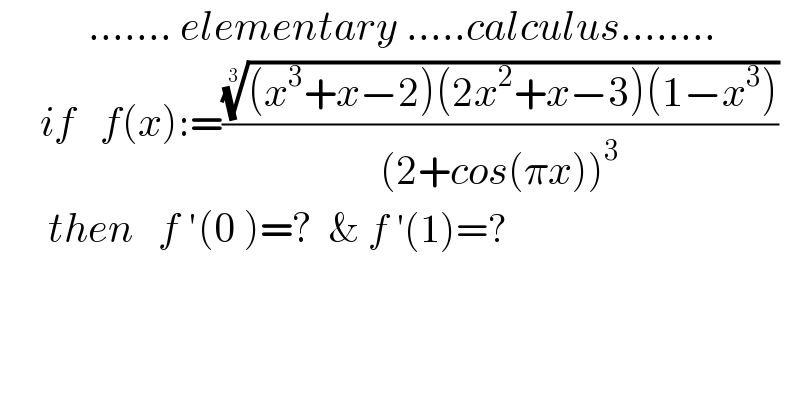
$$\:\:\:\:\:\:\:\:\:\:\:…….\:{elementary}\:…..{calculus}…….. \\ $$$$\:\:\:\:\:{if}\:\:\:{f}\left({x}\right):=\frac{\sqrt[{\mathrm{3}}]{\left({x}^{\mathrm{3}} +{x}−\mathrm{2}\right)\left(\mathrm{2}{x}^{\mathrm{2}} +{x}−\mathrm{3}\right)\left(\mathrm{1}−{x}^{\mathrm{3}} \right)}}{\left(\mathrm{2}+{cos}\left(\pi{x}\right)\right)^{\mathrm{3}} } \\ $$$$\:\:\:\:\:\:{then}\:\:\:{f}\:'\left(\mathrm{0}\:\right)=?\:\:\&\:{f}\:'\left(\mathrm{1}\right)=? \\ $$$$ \\ $$
Answered by mindispower last updated on 17/May/21
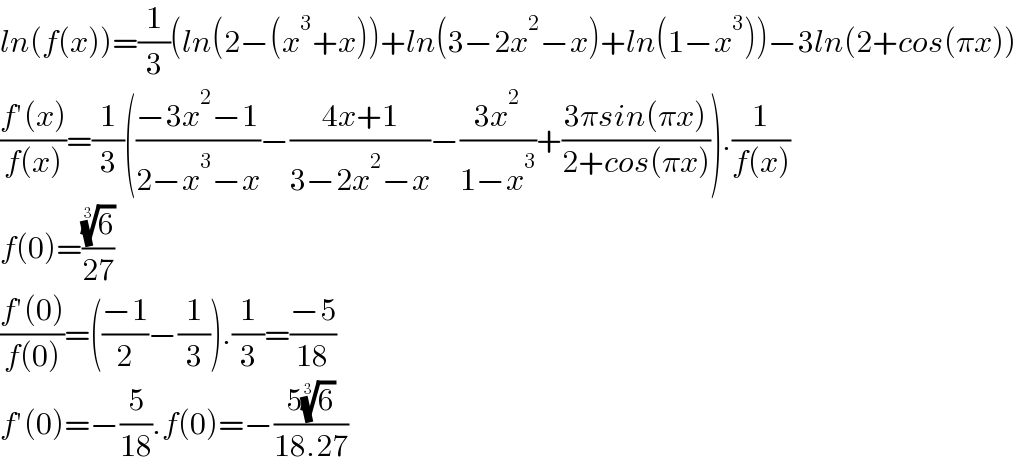
$${ln}\left({f}\left({x}\right)\right)=\frac{\mathrm{1}}{\mathrm{3}}\left({ln}\left(\mathrm{2}−\left({x}^{\mathrm{3}} +{x}\right)\right)+{ln}\left(\mathrm{3}−\mathrm{2}{x}^{\mathrm{2}} −{x}\right)+{ln}\left(\mathrm{1}−{x}^{\mathrm{3}} \right)\right)−\mathrm{3}{ln}\left(\mathrm{2}+{cos}\left(\pi{x}\right)\right) \\ $$$$\frac{{f}'\left({x}\right)}{{f}\left({x}\right)}=\frac{\mathrm{1}}{\mathrm{3}}\left(\frac{−\mathrm{3}{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}−{x}^{\mathrm{3}} −{x}}−\frac{\mathrm{4}{x}+\mathrm{1}}{\mathrm{3}−\mathrm{2}{x}^{\mathrm{2}} −{x}}−\frac{\mathrm{3}{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{3}} }+\frac{\mathrm{3}\pi{sin}\left(\pi{x}\right)}{\mathrm{2}+{cos}\left(\pi{x}\right)}\right).\frac{\mathrm{1}}{{f}\left({x}\right)} \\ $$$${f}\left(\mathrm{0}\right)=\frac{\sqrt[{\mathrm{3}}]{\mathrm{6}}}{\mathrm{27}} \\ $$$$\frac{{f}'\left(\mathrm{0}\right)}{{f}\left(\mathrm{0}\right)}=\left(\frac{−\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{3}}\right).\frac{\mathrm{1}}{\mathrm{3}}=\frac{−\mathrm{5}}{\mathrm{18}} \\ $$$${f}'\left(\mathrm{0}\right)=−\frac{\mathrm{5}}{\mathrm{18}}.{f}\left(\mathrm{0}\right)=−\frac{\mathrm{5}\sqrt[{\mathrm{3}}]{\mathrm{6}}}{\mathrm{18}.\mathrm{27}} \\ $$
Commented by mnjuly1970 last updated on 17/May/21

$$\:{grateful}…. \\ $$
Commented by mindispower last updated on 17/May/21

$${pleasur} \\ $$
