Question Number 139924 by EDWIN88 last updated on 02/May/21
![Evaluate ∫_((0,1)) ^((1,2)) [ (x^2 −y)dx + (y^2 +x) dy ] along a straight line from (0,1) to (1,2).](https://www.tinkutara.com/question/Q139924.png)
$$\:\:\:\:\:\:\mathrm{Evaluate}\:\int_{\left(\mathrm{0},\mathrm{1}\right)} ^{\left(\mathrm{1},\mathrm{2}\right)} \:\left[\:\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}\right)\mathrm{dx}\:+\:\left(\mathrm{y}^{\mathrm{2}} +\mathrm{x}\right)\:\mathrm{dy}\:\right]\: \\ $$$$\mathrm{along}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}\:\mathrm{from}\:\left(\mathrm{0},\mathrm{1}\right)\:\mathrm{to}\:\left(\mathrm{1},\mathrm{2}\right). \\ $$
Answered by TheSupreme last updated on 02/May/21
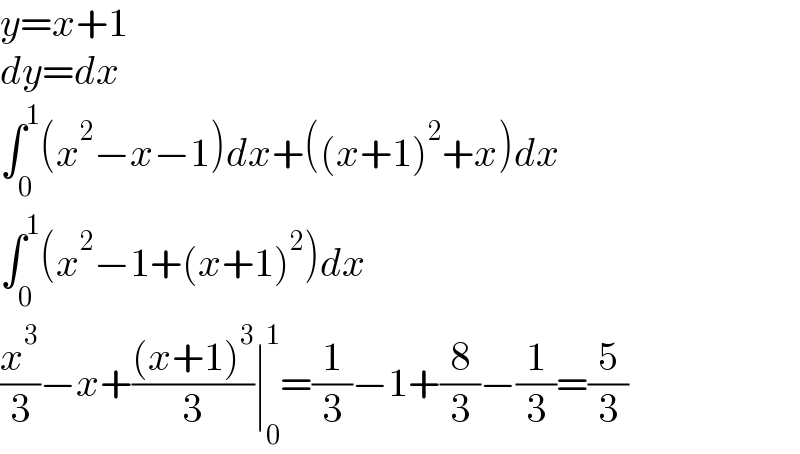
$${y}={x}+\mathrm{1} \\ $$$${dy}={dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{\mathrm{2}} −{x}−\mathrm{1}\right){dx}+\left(\left({x}+\mathrm{1}\right)^{\mathrm{2}} +{x}\right){dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{\mathrm{2}} −\mathrm{1}+\left({x}+\mathrm{1}\right)^{\mathrm{2}} \right){dx} \\ $$$$\frac{{x}^{\mathrm{3}} }{\mathrm{3}}−{x}+\frac{\left({x}+\mathrm{1}\right)^{\mathrm{3}} }{\mathrm{3}}\mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{3}}−\mathrm{1}+\frac{\mathrm{8}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$
Commented by MJS_new last updated on 02/May/21
![y=x+1 x^2 −(x+1)+(x+1)^2 +x=2(x^2 +x) dy=dx 2∫_0 ^1 (x^2 +x)dx=[(2/3)x^3 +x^2 ]_0 ^1 =(5/3)](https://www.tinkutara.com/question/Q139935.png)
$${y}={x}+\mathrm{1} \\ $$$${x}^{\mathrm{2}} −\left({x}+\mathrm{1}\right)+\left({x}+\mathrm{1}\right)^{\mathrm{2}} +{x}=\mathrm{2}\left({x}^{\mathrm{2}} +{x}\right) \\ $$$${dy}={dx} \\ $$$$\mathrm{2}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({x}^{\mathrm{2}} +{x}\right){dx}=\left[\frac{\mathrm{2}}{\mathrm{3}}{x}^{\mathrm{3}} +{x}^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{5}}{\mathrm{3}} \\ $$
