Question Number 142791 by mnjuly1970 last updated on 05/Jun/21
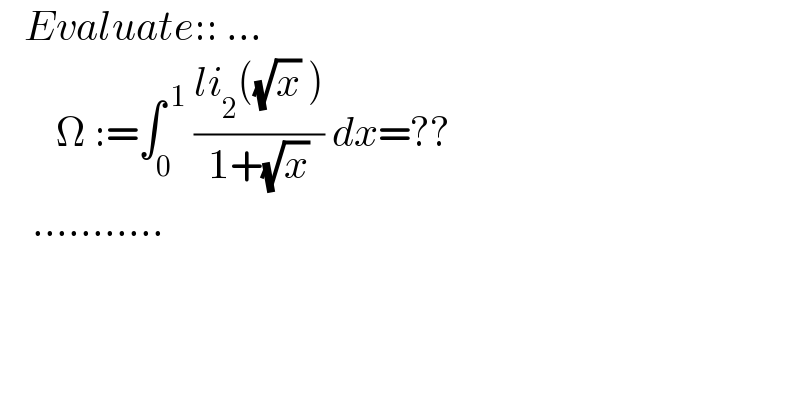
$$\:\:\:{Evaluate}::\:… \\ $$$$\:\:\:\:\:\:\:\Omega\::=\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\frac{{li}_{\mathrm{2}} \left(\sqrt{{x}}\:\right)}{\mathrm{1}+\sqrt{{x}}}\:{dx}=?? \\ $$$$\:\:\:\:……….. \\ $$
Answered by Dwaipayan Shikari last updated on 05/Jun/21
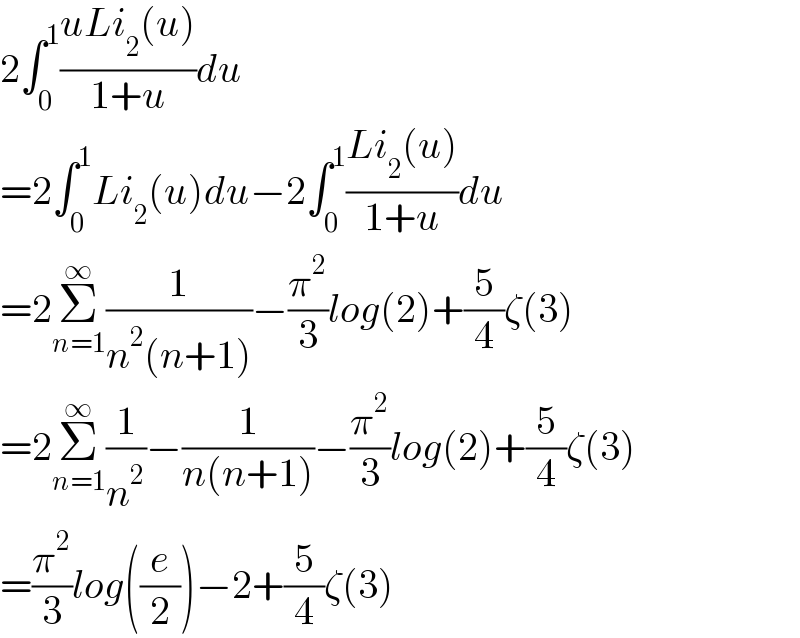
$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{uLi}_{\mathrm{2}} \left({u}\right)}{\mathrm{1}+{u}}{du} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} {Li}_{\mathrm{2}} \left({u}\right){du}−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Li}_{\mathrm{2}} \left({u}\right)}{\mathrm{1}+{u}}{du} \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)}−\frac{\pi^{\mathrm{2}} }{\mathrm{3}}{log}\left(\mathrm{2}\right)+\frac{\mathrm{5}}{\mathrm{4}}\zeta\left(\mathrm{3}\right) \\ $$$$=\mathrm{2}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)}−\frac{\pi^{\mathrm{2}} }{\mathrm{3}}{log}\left(\mathrm{2}\right)+\frac{\mathrm{5}}{\mathrm{4}}\zeta\left(\mathrm{3}\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{3}}{log}\left(\frac{{e}}{\mathrm{2}}\right)−\mathrm{2}+\frac{\mathrm{5}}{\mathrm{4}}\zeta\left(\mathrm{3}\right) \\ $$
Commented by mnjuly1970 last updated on 05/Jun/21
$$\:\:{tashakor}\:{and}\:{sepas}\:{mr}\:{payan}… \\ $$
