Question Number 12101 by Nayon last updated on 13/Apr/17
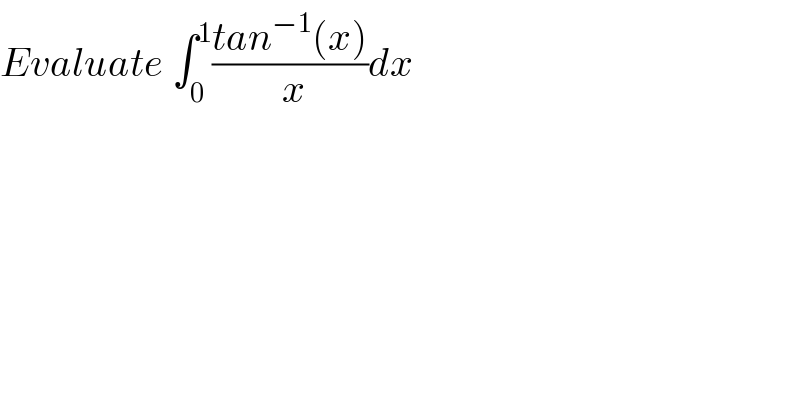
$${Evaluate}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{tan}^{−\mathrm{1}} \left({x}\right)}{\:{x}}{dx} \\ $$
Answered by b.e.h.i.8.3.4.1.7@gmail.com last updated on 13/Apr/17
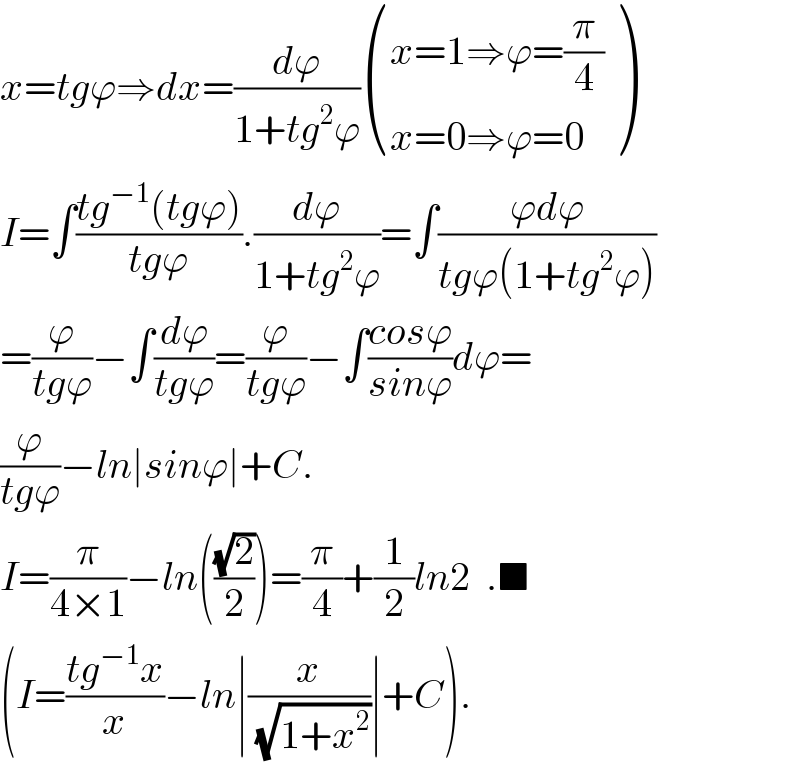
$${x}={tg}\varphi\Rightarrow{dx}=\frac{{d}\varphi}{\mathrm{1}+{tg}^{\mathrm{2}} \varphi}\begin{pmatrix}{{x}=\mathrm{1}\Rightarrow\varphi=\frac{\pi}{\mathrm{4}}}\\{{x}=\mathrm{0}\Rightarrow\varphi=\mathrm{0}}\end{pmatrix} \\ $$$${I}=\int\frac{{tg}^{−\mathrm{1}} \left({tg}\varphi\right)}{{tg}\varphi}.\frac{{d}\varphi}{\mathrm{1}+{tg}^{\mathrm{2}} \varphi}=\int\frac{\varphi{d}\varphi}{{tg}\varphi\left(\mathrm{1}+{tg}^{\mathrm{2}} \varphi\right)} \\ $$$$=\frac{\varphi}{{tg}\varphi}−\int\frac{{d}\varphi}{{tg}\varphi}=\frac{\varphi}{{tg}\varphi}−\int\frac{{cos}\varphi}{{sin}\varphi}{d}\varphi= \\ $$$$\frac{\varphi}{{tg}\varphi}−{ln}\mid{sin}\varphi\mid+{C}. \\ $$$${I}=\frac{\pi}{\mathrm{4}×\mathrm{1}}−{ln}\left(\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right)=\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2}\:\:.\blacksquare \\ $$$$\left({I}=\frac{{tg}^{−\mathrm{1}} {x}}{{x}}−{ln}\mid\frac{{x}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\mid+{C}\right). \\ $$
