Question Number 6204 by sanusihammed last updated on 18/Jun/16
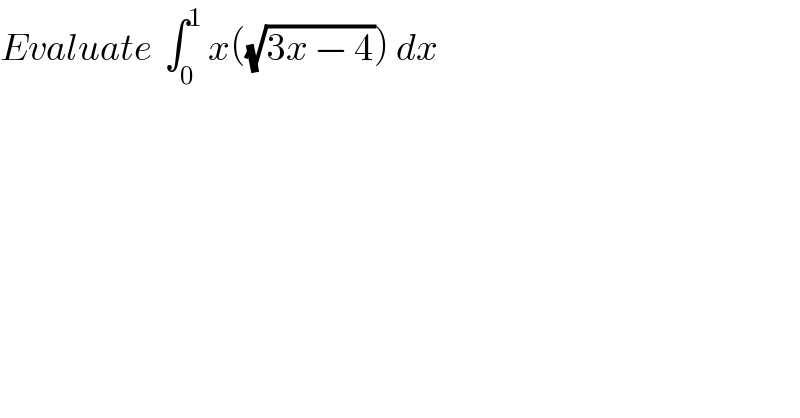
$${Evaluate}\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\left(\sqrt{\mathrm{3}{x}\:−\:\mathrm{4}}\right)\:{dx} \\ $$
Answered by FilupSmith last updated on 18/Jun/16
![u=3x−4 ⇒ du=3dx → dx=(1/3)du x=(1/3)(u+4) =∫_(x=0) ^( x=1) (1/3)(u+4)(√u)(1/3)du =(1/9)∫_(x=0) ^( x=1) (u(√u)+4(√u))du =(1/9)(∫_(x=0) ^( x=1) (u(√u))du+∫_(x=0) ^( x=1) (4(√u))du) =(1/9)(∫_(x=0) ^( x=1) (u^(3/2) )du+4∫_(x=0) ^( x=1) ((√u))du) =(1/9)([(2/5)u^(5/2) ]_(x=0) ^(x=1) +4[(2/3)u^(3/2) ]_(x=0) ^(x=1) ) =(1/9)([(2/5)(3x−4)^(5/2) ]_0 ^1 +4[(2/3)(3x−4)^(3/2) ]_0 ^1 ) =(1/9)((2/5)((3−4)^(5/2) −(−4)^(5/2) )+(8/3)((3−4)^(3/2) −(−4)^(3/2) )) =(1/9)((2/5)(i−32i)+(8/3)((−i)−(−8i))) =(1/9)((2/5)(−31i)+(8/3)(7i)) =(1/9)(((−62i)/5)+((56i)/3)) =(1/9)(((−186i+280i)/(15))) =((−186i+280i)/(135)) =((94i)/(135)) ∴ ∫_0 ^1 x((√(3x − 4))) dx = ((94i)/(135)) where i^2 =−1](https://www.tinkutara.com/question/Q6211.png)
$${u}=\mathrm{3}{x}−\mathrm{4}\:\Rightarrow\:{du}=\mathrm{3}{dx}\:\rightarrow\:{dx}=\frac{\mathrm{1}}{\mathrm{3}}{du} \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{3}}\left({u}+\mathrm{4}\right) \\ $$$$=\int_{{x}=\mathrm{0}} ^{\:{x}=\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}}\left({u}+\mathrm{4}\right)\sqrt{{u}}\frac{\mathrm{1}}{\mathrm{3}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\int_{{x}=\mathrm{0}} ^{\:{x}=\mathrm{1}} \left({u}\sqrt{{u}}+\mathrm{4}\sqrt{{u}}\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\int_{{x}=\mathrm{0}} ^{\:{x}=\mathrm{1}} \left({u}\sqrt{{u}}\right){du}+\int_{{x}=\mathrm{0}} ^{\:{x}=\mathrm{1}} \left(\mathrm{4}\sqrt{{u}}\right){du}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\int_{{x}=\mathrm{0}} ^{\:{x}=\mathrm{1}} \left({u}^{\mathrm{3}/\mathrm{2}} \right){du}+\mathrm{4}\int_{{x}=\mathrm{0}} ^{\:{x}=\mathrm{1}} \left(\sqrt{{u}}\right){du}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\left[\frac{\mathrm{2}}{\mathrm{5}}{u}^{\mathrm{5}/\mathrm{2}} \right]_{{x}=\mathrm{0}} ^{{x}=\mathrm{1}} +\mathrm{4}\left[\frac{\mathrm{2}}{\mathrm{3}}{u}^{\mathrm{3}/\mathrm{2}} \right]_{{x}=\mathrm{0}} ^{{x}=\mathrm{1}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\left[\frac{\mathrm{2}}{\mathrm{5}}\left(\mathrm{3}{x}−\mathrm{4}\right)^{\mathrm{5}/\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} +\mathrm{4}\left[\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{3}{x}−\mathrm{4}\right)^{\mathrm{3}/\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} \right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\frac{\mathrm{2}}{\mathrm{5}}\left(\left(\mathrm{3}−\mathrm{4}\right)^{\mathrm{5}/\mathrm{2}} −\left(−\mathrm{4}\right)^{\mathrm{5}/\mathrm{2}} \right)+\frac{\mathrm{8}}{\mathrm{3}}\left(\left(\mathrm{3}−\mathrm{4}\right)^{\mathrm{3}/\mathrm{2}} −\left(−\mathrm{4}\right)^{\mathrm{3}/\mathrm{2}} \right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\frac{\mathrm{2}}{\mathrm{5}}\left({i}−\mathrm{32}{i}\right)+\frac{\mathrm{8}}{\mathrm{3}}\left(\left(−{i}\right)−\left(−\mathrm{8}{i}\right)\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\frac{\mathrm{2}}{\mathrm{5}}\left(−\mathrm{31}{i}\right)+\frac{\mathrm{8}}{\mathrm{3}}\left(\mathrm{7}{i}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\frac{−\mathrm{62}{i}}{\mathrm{5}}+\frac{\mathrm{56}{i}}{\mathrm{3}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{9}}\left(\frac{−\mathrm{186}{i}+\mathrm{280}{i}}{\mathrm{15}}\right) \\ $$$$=\frac{−\mathrm{186}{i}+\mathrm{280}{i}}{\mathrm{135}} \\ $$$$=\frac{\mathrm{94}{i}}{\mathrm{135}} \\ $$$$ \\ $$$$\therefore\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\left(\sqrt{\mathrm{3}{x}\:−\:\mathrm{4}}\right)\:{dx}\:=\:\frac{\mathrm{94}{i}}{\mathrm{135}} \\ $$$$\mathrm{where}\:\:{i}^{\mathrm{2}} =−\mathrm{1} \\ $$
Commented by sanusihammed last updated on 18/Jun/16

$${Thanks}\:{so}\:{much} \\ $$
