Question Number 66561 by Rio Michael last updated on 17/Aug/19

$${evaluate}\: \\ $$$$\:\:\int_{\mathrm{0}} ^{\mathrm{2}} \mid\:{x}+\:\mathrm{2}\mid\:{dx}. \\ $$
Commented by kaivan.ahmadi last updated on 17/Aug/19

$$\mathrm{0}<{x}<\mathrm{2}\Rightarrow{x}+\mathrm{2}>\mathrm{0}\Rightarrow\mid{x}+\mathrm{2}\mid={x}+\mathrm{2} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \left({x}+\mathrm{2}\right){dx}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}{x}\mid_{\mathrm{0}} ^{\mathrm{2}} =\left(\mathrm{2}+\mathrm{4}\right)−\mathrm{0}=\mathrm{6} \\ $$
Commented by Rio Michael last updated on 17/Aug/19
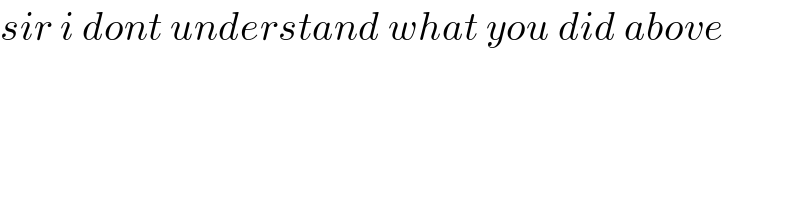
$${sir}\:{i}\:{dont}\:{understand}\:{what}\:{you}\:{did}\:{above} \\ $$
Answered by Tanmay chaudhury last updated on 17/Aug/19

$$\mid{x}+\mathrm{2}\mid \\ $$$$={x}+\mathrm{2}\:\:\:{sinc}\:{here}\:{interval}\:{from}\:\:\mathrm{0}\:{to}\:\mathrm{2} \\ $$$${so}\:{x}\:{is}\:{positive} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{2}} \left({x}+\mathrm{2}\right){dx} \\ $$$$\mid\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}{x}\mid_{\mathrm{0}} ^{\mathrm{2}} \\ $$$$=\frac{\mathrm{4}}{\mathrm{2}}+\mathrm{2}×\mathrm{2} \\ $$$$=\mathrm{6} \\ $$
Commented by Rio Michael last updated on 17/Aug/19

$${thanks}\:{so}\:{how}\:{do}\:{i}\:{solve}\:{this}\:{then} \\ $$$$\int_{\mathrm{2}} ^{\mathrm{3}} \:\mid\:{x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}\mid\:{dx}? \\ $$
Commented by mr W last updated on 17/Aug/19
![∫_2 ^3 .... means the range for x is [2,3]. in the range 2≤x≤3 it′s clear that x^2 +x+1>0, hence ∣x^2 +x+1∣=x^2 +x+1, ∫_2 ^3 ∣ x^2 + x + 1∣ dx =∫_2 ^3 (x^2 + x + 1)dx =[(x^3 /3)+(x^2 /2)+x]_2 ^3 =[(3^3 /3)+(3^2 /2)+3]−[(2^3 /3)+(2^2 /2)+2] =((27−8)/3)+((9−4)/2)+3−2 =((19)/3)+(5/2)+1 =((19×2+5×3+6)/6) =((59)/6)](https://www.tinkutara.com/question/Q66617.png)
$$\int_{\mathrm{2}} ^{\mathrm{3}} ….\:{means}\:{the}\:{range}\:{for}\:{x}\:{is}\:\left[\mathrm{2},\mathrm{3}\right]. \\ $$$${in}\:{the}\:{range}\:\mathrm{2}\leqslant{x}\leqslant\mathrm{3}\:{it}'{s}\:{clear}\:{that} \\ $$$${x}^{\mathrm{2}} +{x}+\mathrm{1}>\mathrm{0},\:{hence}\:\mid{x}^{\mathrm{2}} +{x}+\mathrm{1}\mid={x}^{\mathrm{2}} +{x}+\mathrm{1}, \\ $$$$\int_{\mathrm{2}} ^{\mathrm{3}} \:\mid\:{x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}\mid\:{dx} \\ $$$$=\int_{\mathrm{2}} ^{\mathrm{3}} \:\left({x}^{\mathrm{2}} \:+\:{x}\:+\:\mathrm{1}\right){dx} \\ $$$$=\left[\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}+{x}\right]_{\mathrm{2}} ^{\mathrm{3}} \\ $$$$=\left[\frac{\mathrm{3}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{3}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{3}\right]−\left[\frac{\mathrm{2}^{\mathrm{3}} }{\mathrm{3}}+\frac{\mathrm{2}^{\mathrm{2}} }{\mathrm{2}}+\mathrm{2}\right] \\ $$$$=\frac{\mathrm{27}−\mathrm{8}}{\mathrm{3}}+\frac{\mathrm{9}−\mathrm{4}}{\mathrm{2}}+\mathrm{3}−\mathrm{2} \\ $$$$=\frac{\mathrm{19}}{\mathrm{3}}+\frac{\mathrm{5}}{\mathrm{2}}+\mathrm{1} \\ $$$$=\frac{\mathrm{19}×\mathrm{2}+\mathrm{5}×\mathrm{3}+\mathrm{6}}{\mathrm{6}} \\ $$$$=\frac{\mathrm{59}}{\mathrm{6}} \\ $$
Commented by Rio Michael last updated on 17/Aug/19

$${thank}\:{you} \\ $$
