Question Number 135932 by Engr_Jidda last updated on 17/Mar/21
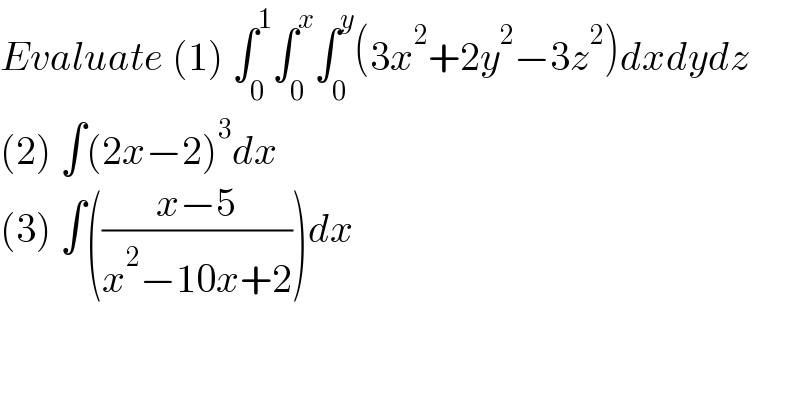
$${Evaluate}\:\left(\mathrm{1}\right)\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{{x}} \int_{\mathrm{0}} ^{{y}} \left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} −\mathrm{3}{z}^{\mathrm{2}} \right){dxdydz} \\ $$$$\left(\mathrm{2}\right)\:\int\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{3}} {dx} \\ $$$$\left(\mathrm{3}\right)\:\int\left(\frac{{x}−\mathrm{5}}{{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{2}}\right){dx} \\ $$
Answered by Olaf last updated on 17/Mar/21
![1) Ω = ∫_0 ^1 ∫_0 ^x ∫_0 ^y (3x^2 +2y^2 −3z^2 )dxdydz Ω = ∫_0 ^1 ∫_0 ^x [3x^2 z+2y^2 z−z^3 ]_0 ^y dxdy Ω = ∫_0 ^1 ∫_0 ^x (3x^2 y+y^3 )dxdy Ω = ∫_0 ^1 [(3/2)x^2 y^2 +(y^4 /4)]_0 ^x dx Ω = ∫_0 ^1 (7/4)x^4 dx = (7/4) 2) ∫(2x−2)^3 dx = (1/8)(2x−2)^4 +C = 2(x−1)^4 +C 3) ∫((x−5)/(x^2 −10x+2))dx = (1/2)∫ ((d(x^2 −10x+2))/(x^2 −10x+2)) = (1/2)ln∣x^2 −10x+2∣+C](https://www.tinkutara.com/question/Q135938.png)
$$\left.\mathrm{1}\right) \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{{x}} \int_{\mathrm{0}} ^{{y}} \left(\mathrm{3}{x}^{\mathrm{2}} +\mathrm{2}{y}^{\mathrm{2}} −\mathrm{3}{z}^{\mathrm{2}} \right){dxdydz} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{{x}} \left[\mathrm{3}{x}^{\mathrm{2}} {z}+\mathrm{2}{y}^{\mathrm{2}} {z}−{z}^{\mathrm{3}} \right]_{\mathrm{0}} ^{{y}} {dxdy} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \int_{\mathrm{0}} ^{{x}} \left(\mathrm{3}{x}^{\mathrm{2}} {y}+{y}^{\mathrm{3}} \right){dxdy} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \left[\frac{\mathrm{3}}{\mathrm{2}}{x}^{\mathrm{2}} {y}^{\mathrm{2}} +\frac{{y}^{\mathrm{4}} }{\mathrm{4}}\right]_{\mathrm{0}} ^{{x}} {dx} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{7}}{\mathrm{4}}{x}^{\mathrm{4}} {dx}\:=\:\frac{\mathrm{7}}{\mathrm{4}} \\ $$$$\left.\mathrm{2}\right) \\ $$$$\int\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{3}} {dx}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\left(\mathrm{2}{x}−\mathrm{2}\right)^{\mathrm{4}} +\mathrm{C}\:=\:\mathrm{2}\left({x}−\mathrm{1}\right)^{\mathrm{4}} +\mathrm{C} \\ $$$$\left.\mathrm{3}\right) \\ $$$$\int\frac{{x}−\mathrm{5}}{{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{2}}{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\int\:\frac{{d}\left({x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{2}\right)}{{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\mid{x}^{\mathrm{2}} −\mathrm{10}{x}+\mathrm{2}\mid+\mathrm{C} \\ $$
Answered by Ar Brandon last updated on 17/Mar/21
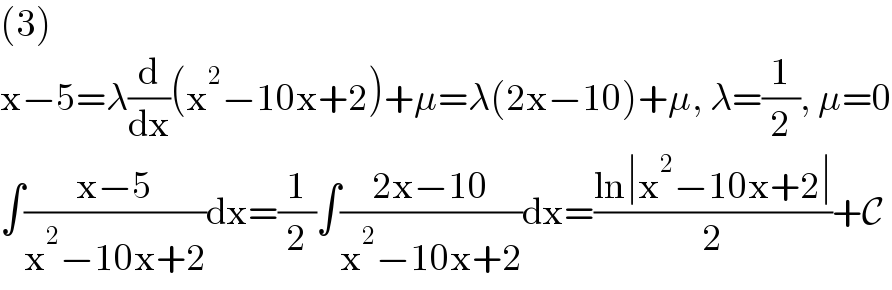
$$\left(\mathrm{3}\right) \\ $$$$\mathrm{x}−\mathrm{5}=\lambda\frac{\mathrm{d}}{\mathrm{dx}}\left(\mathrm{x}^{\mathrm{2}} −\mathrm{10x}+\mathrm{2}\right)+\mu=\lambda\left(\mathrm{2x}−\mathrm{10}\right)+\mu,\:\lambda=\frac{\mathrm{1}}{\mathrm{2}},\:\mu=\mathrm{0} \\ $$$$\int\frac{\mathrm{x}−\mathrm{5}}{\mathrm{x}^{\mathrm{2}} −\mathrm{10x}+\mathrm{2}}\mathrm{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2x}−\mathrm{10}}{\mathrm{x}^{\mathrm{2}} −\mathrm{10x}+\mathrm{2}}\mathrm{dx}=\frac{\mathrm{ln}\mid\mathrm{x}^{\mathrm{2}} −\mathrm{10x}+\mathrm{2}\mid}{\mathrm{2}}+\mathcal{C} \\ $$
