Question Number 689 by 112358 last updated on 25/Feb/15

$${Evaluate}\: \\ $$$$\left(\mathrm{1}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\infty} {sin}\left({x}^{\mathrm{2}} \right){dx}, \\ $$$$\left(\mathrm{2}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\infty} {cos}\left({x}^{\mathrm{2}} \right){dx}, \\ $$$$\left(\mathrm{3}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\infty} {tan}\left({x}^{\mathrm{2}} \right){dx}. \\ $$
Commented by 123456 last updated on 25/Feb/15

$$\:\underset{\Gamma} {\int}{e}^{\imath{z}^{\mathrm{2}} } {dz} \\ $$
Answered by prakash jain last updated on 25/Feb/15
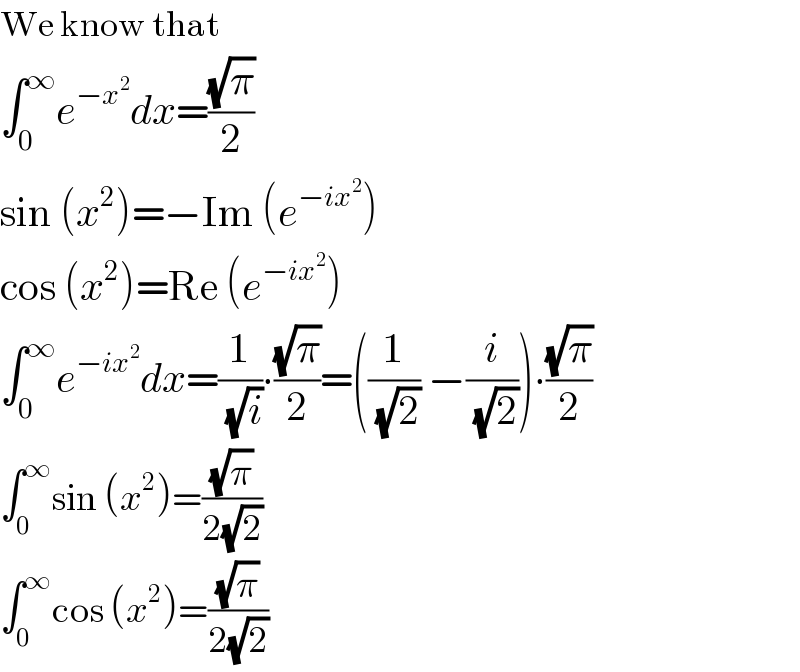
$$\mathrm{We}\:\mathrm{know}\:\mathrm{that} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}=\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\mathrm{sin}\:\left({x}^{\mathrm{2}} \right)=−\mathrm{Im}\:\left({e}^{−{ix}^{\mathrm{2}} } \right) \\ $$$$\mathrm{cos}\:\left({x}^{\mathrm{2}} \right)=\mathrm{Re}\:\left({e}^{−{ix}^{\mathrm{2}} } \right) \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{ix}^{\mathrm{2}} } {dx}=\frac{\mathrm{1}}{\:\sqrt{{i}}}\centerdot\frac{\sqrt{\pi}}{\mathrm{2}}=\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:−\frac{{i}}{\:\sqrt{\mathrm{2}}}\right)\centerdot\frac{\sqrt{\pi}}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \mathrm{sin}\:\left({x}^{\mathrm{2}} \right)=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \mathrm{cos}\:\left({x}^{\mathrm{2}} \right)=\frac{\sqrt{\pi}}{\mathrm{2}\sqrt{\mathrm{2}}} \\ $$
Commented by prakash jain last updated on 25/Feb/15

$$\int_{\mathrm{0}} ^{\infty} \mathrm{tan}\:\left({x}^{\mathrm{2}} \right)\:{dx}\:\mathrm{does}\:\mathrm{not}\:\mathrm{coverge}.\: \\ $$
