Question Number 73428 by Learner-123 last updated on 12/Nov/19
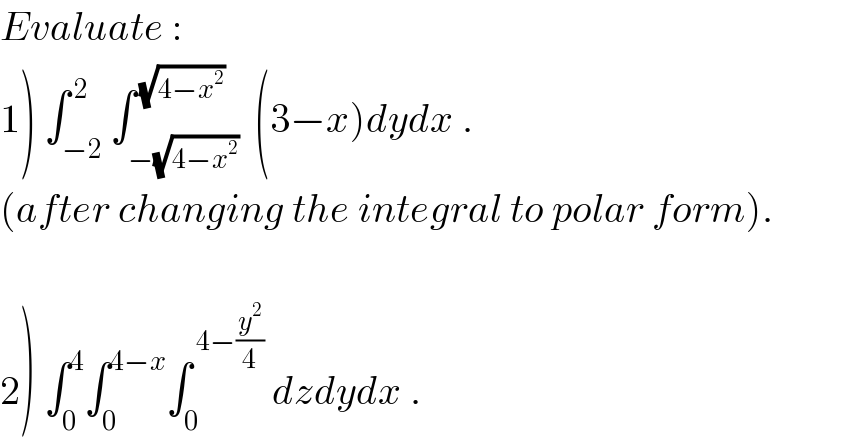
$${Evaluate}\:: \\ $$$$\left.\mathrm{1}\right)\:\int_{−\mathrm{2}} ^{\:\mathrm{2}} \int_{−\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} ^{\:\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} \:\left(\mathrm{3}−{x}\right){dydx}\:. \\ $$$$\left({after}\:{changing}\:{the}\:{integral}\:{to}\:{polar}\:{form}\right). \\ $$$$ \\ $$$$\left.\mathrm{2}\right)\:\int_{\mathrm{0}} ^{\mathrm{4}} \int_{\mathrm{0}} ^{\mathrm{4}−{x}} \int_{\mathrm{0}} ^{\:\mathrm{4}−\frac{{y}^{\mathrm{2}} }{\mathrm{4}}} \:{dzdydx}\:. \\ $$
Commented by mathmax by abdo last updated on 12/Nov/19
![1) I =∫_(−2) ^2 (∫_(−(√(4−x^2 ))) ^(√(4−x^2 )) dy)(3−x)dx =∫_(−2) ^2 2(√(4−x^2 ))(3−x)dx =2 ∫_(−2) ^2 (3−x)(√(4−x^2 )) dx =_(x=2sinθ) 2 ∫_(−(π/2)) ^(π/2) (3−2sinθ)2cosθ (2cosθ)dθ =8 ∫_(−(π/2)) ^(π/2) (3−2sinθ) cos^2 θ dθ =24 ∫_(−(π/2)) ^(π/2) cos^2 θ dθ −16 ∫_(−(π/2)) ^(π/2) sinθ cos^2 θ dθ we have ∫_(−(π/2)) ^(π/2) sinθ cos^2 θ dθ =[−(1/3)cos^3 θ]_(−(π/2)) ^(π/2) =0 ∫_(−(π/2)) ^(π/2) cos^2 θ dθ =2 ∫_0 ^(π/2) ((1+cos(2θ))/2)dθ =(π/2) +∫_0 ^(π/2) cos(2θ)dθ =(π/2) +[(1/2)sin(2θ)]_0 ^(π/2) =(π/2) +0 =(π/2) ⇒I =24×(π/2) ⇒I=12π](https://www.tinkutara.com/question/Q73443.png)
$$\left.\mathrm{1}\right)\:{I}\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \left(\int_{−\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} ^{\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }} {dy}\right)\left(\mathrm{3}−{x}\right){dx}\:=\int_{−\mathrm{2}} ^{\mathrm{2}} \mathrm{2}\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\left(\mathrm{3}−{x}\right){dx} \\ $$$$=\mathrm{2}\:\int_{−\mathrm{2}} ^{\mathrm{2}} \left(\mathrm{3}−{x}\right)\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx}\:\:=_{{x}=\mathrm{2}{sin}\theta} \:\:\:\mathrm{2}\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{3}−\mathrm{2}{sin}\theta\right)\mathrm{2}{cos}\theta\:\left(\mathrm{2}{cos}\theta\right){d}\theta \\ $$$$=\mathrm{8}\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{3}−\mathrm{2}{sin}\theta\right)\:{cos}^{\mathrm{2}} \theta\:{d}\theta\:=\mathrm{24}\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} {cos}^{\mathrm{2}} \theta\:{d}\theta\:−\mathrm{16}\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\theta\:{cos}^{\mathrm{2}} \theta\:{d}\theta \\ $$$${we}\:{have}\:\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}\theta\:{cos}^{\mathrm{2}} \theta\:{d}\theta\:=\left[−\frac{\mathrm{1}}{\mathrm{3}}{cos}^{\mathrm{3}} \theta\right]_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} =\mathrm{0} \\ $$$$\int_{−\frac{\pi}{\mathrm{2}}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}} \theta\:{d}\theta\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+{cos}\left(\mathrm{2}\theta\right)}{\mathrm{2}}{d}\theta\:=\frac{\pi}{\mathrm{2}}\:+\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}\theta\right){d}\theta \\ $$$$=\frac{\pi}{\mathrm{2}}\:+\left[\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\pi}{\mathrm{2}}\:+\mathrm{0}\:=\frac{\pi}{\mathrm{2}}\:\Rightarrow{I}\:=\mathrm{24}×\frac{\pi}{\mathrm{2}}\:\Rightarrow{I}=\mathrm{12}\pi \\ $$
Commented by Learner-123 last updated on 12/Nov/19

$${thnks}\:{sir}. \\ $$
Answered by Henri Boucatchou last updated on 12/Nov/19
![1) I =∫_(−2) ^( 2) 2(3−x)(√(4−x^2 )) dx x=2cosθ, −1≤cosθ≤1, dx=−2sinθdθ I = 4∫_(−π) ^( 0) (3−2cosθ)∣sinθ∣(−2sinθ)dθ =8[∫_(−π) ^( 0) (3−2cosθ)sin^2 θdθ] =8[3∫_(−π) ^( 0) sin^2 θdθ − 2∫_(−π) ^( 0) cosθsin^2 θdθ] =8[(3/2)∫_(−π) ^( 0) (1−cos2θ)dθ − 2.0] =8.(3/2)[θ−(1/2)sin2θ]_(−π) ^0 = 12π −−−−−−−−−−−−−−− ∫_0 ^( 4) ∫_0 ^( 4−x) ∫_0 ^( 4−y^2 /4) dzdydx= ∫_0 ^( 4) ∫_0 ^( 4−x) (4−(y^2 /4))dydx = ∫_0 ^( 4) [4y−(y^3 /(12))]_0 ^(4−x) dx = ∫_0 ^( 4) (4(4−x)−(1/(12))(4−x)^3 )dx = 4(x−(1/2)x^2 )+(1/(12.4))(4−x)^4 ]_0 ^4 = 4(4−(1/2)4^2 )−(1/(12)) = −16−(1/(12)) = −((193)/(12)) PLEASE CHECK IF THERE′S NO ERROR](https://www.tinkutara.com/question/Q73436.png)
$$\left.\mathrm{1}\right)\:\:{I}\:=\int_{−\mathrm{2}} ^{\:\mathrm{2}} \mathrm{2}\left(\mathrm{3}−{x}\right)\sqrt{\mathrm{4}−{x}^{\mathrm{2}} }\:{dx} \\ $$$$\:\:\:{x}=\mathrm{2}{cos}\theta,\:\:−\mathrm{1}\leqslant{cos}\theta\leqslant\mathrm{1},\:\:{dx}=−\mathrm{2}{sin}\theta{d}\theta \\ $$$$\:\:\:{I}\:=\:\mathrm{4}\int_{−\pi} ^{\:\mathrm{0}} \left(\mathrm{3}−\mathrm{2}{cos}\theta\right)\mid{sin}\theta\mid\left(−\mathrm{2}{sin}\theta\right){d}\theta \\ $$$$\:\:\:\:\:\:\:=\mathrm{8}\left[\int_{−\pi} ^{\:\mathrm{0}} \left(\mathrm{3}−\mathrm{2}{cos}\theta\right){sin}^{\mathrm{2}} \theta{d}\theta\right] \\ $$$$\:\:\:\:\:\:\:=\mathrm{8}\left[\mathrm{3}\int_{−\pi} ^{\:\mathrm{0}} {sin}^{\mathrm{2}} \theta{d}\theta\:−\:\mathrm{2}\int_{−\pi} ^{\:\mathrm{0}} {cos}\theta{sin}^{\mathrm{2}} \theta{d}\theta\right] \\ $$$$\:\:\:\:\:\:\:=\mathrm{8}\left[\frac{\mathrm{3}}{\mathrm{2}}\int_{−\pi} ^{\:\mathrm{0}} \left(\mathrm{1}−{cos}\mathrm{2}\theta\right){d}\theta\:−\:\mathrm{2}.\mathrm{0}\right] \\ $$$$\:\:\:\:\:\:\:=\mathrm{8}.\frac{\mathrm{3}}{\mathrm{2}}\left[\theta−\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}\theta\right]_{−\pi} ^{\mathrm{0}} \\ $$$$\:\:\:\:\:\:\:\:=\:\mathrm{12}\pi \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{4}} \int_{\mathrm{0}} ^{\:\mathrm{4}−{x}} \int_{\mathrm{0}} ^{\:\mathrm{4}−{y}^{\mathrm{2}} /\mathrm{4}} {dzdydx}= \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\mathrm{4}} \int_{\mathrm{0}} ^{\:\mathrm{4}−{x}} \left(\mathrm{4}−\frac{{y}^{\mathrm{2}} }{\mathrm{4}}\right){dydx}\:= \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\mathrm{4}} \left[\mathrm{4}{y}−\frac{{y}^{\mathrm{3}} }{\mathrm{12}}\right]_{\mathrm{0}} ^{\mathrm{4}−{x}} {dx}\:= \\ $$$$\:\:\int_{\mathrm{0}} ^{\:\mathrm{4}} \left(\mathrm{4}\left(\mathrm{4}−{x}\right)−\frac{\mathrm{1}}{\mathrm{12}}\left(\mathrm{4}−{x}\right)^{\mathrm{3}} \right){dx}\:= \\ $$$$\left.\:\:\mathrm{4}\left({x}−\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} \right)+\frac{\mathrm{1}}{\mathrm{12}.\mathrm{4}}\left(\mathrm{4}−{x}\right)^{\mathrm{4}} \right]_{\mathrm{0}} ^{\mathrm{4}} \:= \\ $$$$\:\:\mathrm{4}\left(\mathrm{4}−\frac{\mathrm{1}}{\mathrm{2}}\mathrm{4}^{\mathrm{2}} \right)−\frac{\mathrm{1}}{\mathrm{12}}\:= \\ $$$$\:\:\:−\mathrm{16}−\frac{\mathrm{1}}{\mathrm{12}}\:= \\ $$$$\:\:−\frac{\mathrm{193}}{\mathrm{12}} \\ $$$$ \\ $$$$\:\:\boldsymbol{{PLEASE}}\:\:\boldsymbol{{CHECK}}\:\:\boldsymbol{{IF}}\:\:\boldsymbol{{THERE}}'\boldsymbol{{S}}\:\:\boldsymbol{{NO}}\:\:\boldsymbol{{ERROR}} \\ $$$$ \\ $$
Commented by Learner-123 last updated on 12/Nov/19
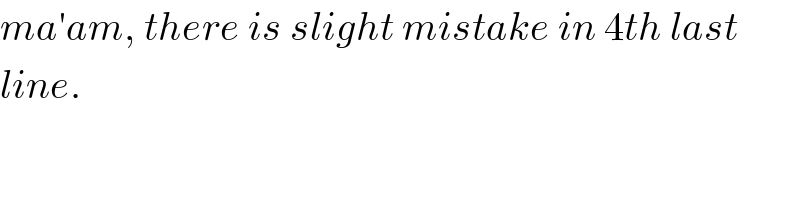
$${ma}'{am},\:{there}\:{is}\:{slight}\:{mistake}\:{in}\:\mathrm{4}{th}\:{last} \\ $$$${line}. \\ $$
