Question Number 11406 by tawa last updated on 24/Mar/17
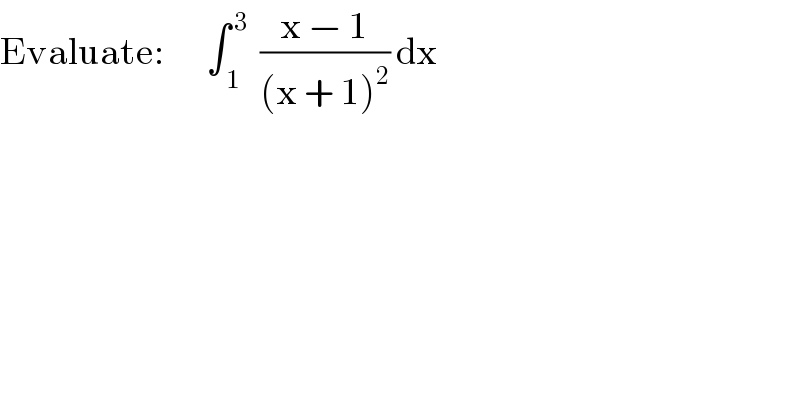
$$\mathrm{Evaluate}:\:\:\:\:\:\:\:\int_{\:\mathrm{1}} ^{\:\mathrm{3}} \:\:\frac{\mathrm{x}\:−\:\mathrm{1}}{\left(\mathrm{x}\:+\:\mathrm{1}\right)^{\mathrm{2}} }\:\mathrm{dx} \\ $$
Answered by sm3l2996 last updated on 24/Mar/17
![((x−1)/((x+1)^2 ))=(a/(x+1))+(b/((x+1)^2 )) b=−2 ; a=1 I=∫_1 ^3 ((x−1)/((x+1)^2 ))dx=∫_1 ^3 (dx/(x+1))−2∫_1 ^3 (dx/((x+1)^2 )) =[ln∣x+1∣]_1 ^3 +2[(1/(x+1))]_1 ^3 =ln(2)−(1/2)](https://www.tinkutara.com/question/Q11407.png)
$$\frac{\mathrm{x}−\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{a}}{\mathrm{x}+\mathrm{1}}+\frac{\mathrm{b}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{b}=−\mathrm{2}\:;\:\mathrm{a}=\mathrm{1} \\ $$$$\mathrm{I}=\int_{\mathrm{1}} ^{\mathrm{3}} \frac{\mathrm{x}−\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}=\int_{\mathrm{1}} ^{\mathrm{3}} \frac{\mathrm{dx}}{\mathrm{x}+\mathrm{1}}−\mathrm{2}\int_{\mathrm{1}} ^{\mathrm{3}} \frac{\mathrm{dx}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=\left[\mathrm{ln}\mid\mathrm{x}+\mathrm{1}\mid\right]_{\mathrm{1}} ^{\mathrm{3}} +\mathrm{2}\left[\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}\right]_{\mathrm{1}} ^{\mathrm{3}} \\ $$$$=\mathrm{ln}\left(\mathrm{2}\right)−\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by tawa last updated on 24/Mar/17

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$
