Question Number 31 by user2 last updated on 25/Jan/15
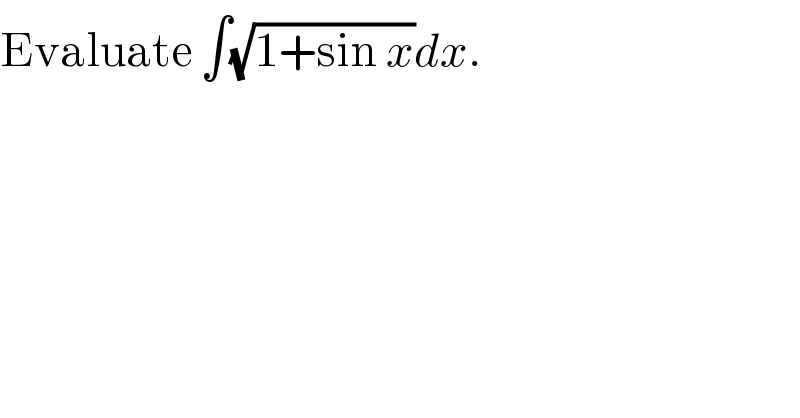
$$\mathrm{Evaluate}\:\int\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}{dx}. \\ $$
Answered by user2 last updated on 03/Nov/14

$$\int\sqrt{\mathrm{1}+\mathrm{sin}\:{x}}\:{dx}=\int\sqrt{\mathrm{sin}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{cos}^{\mathrm{2}} \frac{{x}}{\mathrm{2}}+\mathrm{2sin}\frac{{x}}{\mathrm{2}}\mathrm{cos}\frac{{x}}{\mathrm{2}}\:}{dx} \\ $$$$=\int\left(\mathrm{sin}\frac{{x}}{\mathrm{2}}+\mathrm{cos}\frac{{x}}{\mathrm{2}}\right){dx} \\ $$$$=\int\mathrm{sin}\frac{{x}}{\mathrm{2}}\:{dx}+\int\mathrm{cos}\frac{{x}}{\mathrm{2}}\:{dx} \\ $$$$=−\mathrm{2cos}\frac{{x}}{\mathrm{2}}+\mathrm{2sin}\frac{{x}}{\mathrm{2}}+{C} \\ $$
