evaluate-4-x-dx-

Question Number 8783 by uchechukwu okorie favour last updated on 27/Oct/16

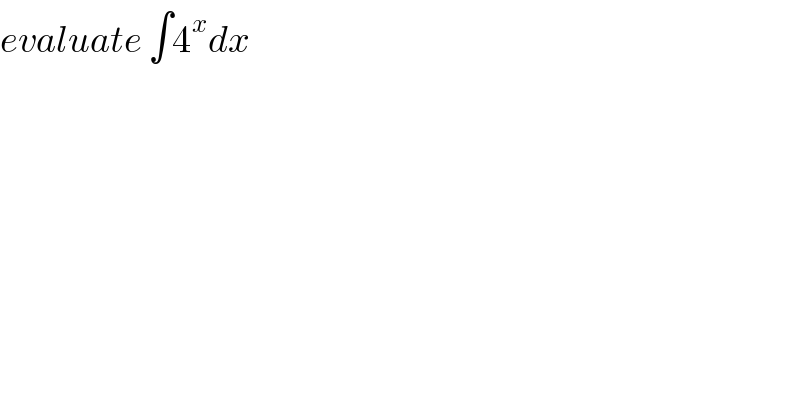
e v a l u a t e \int 4^{x} d x

Answered by FilupSmith last updated on 27/Oct/16

4^{x} = e^{x \ln (4)}

\int 4^{x} d x = \int e^{x \ln (4)} d x

for \int e^{a x + b} d x, a, b = c o n s t a n t s

u = a x + b \Rightarrow d u = a d x

d x = \frac{1}{a} d u

\int e^{a x + b} d x = \int \frac{1}{a} e^{u} d u = \frac{1}{a} e^{u} + C = \frac{1}{a} e^{a x + b} + C, C = c o n s t a n t

\int e^{x \ln (4)} d x = \frac{1}{\ln (4)} e^{x \ln (4)} + C

= \frac{1}{2 \ln (2)} 4^{x} + C (answer)

= \frac{1}{2 \ln (2)} 2^{2 x} + C

= \frac{1}{\ln (2)} 2^{2 x - 1} + C (alternate form)