Question Number 2241 by Yozzi last updated on 10/Nov/15
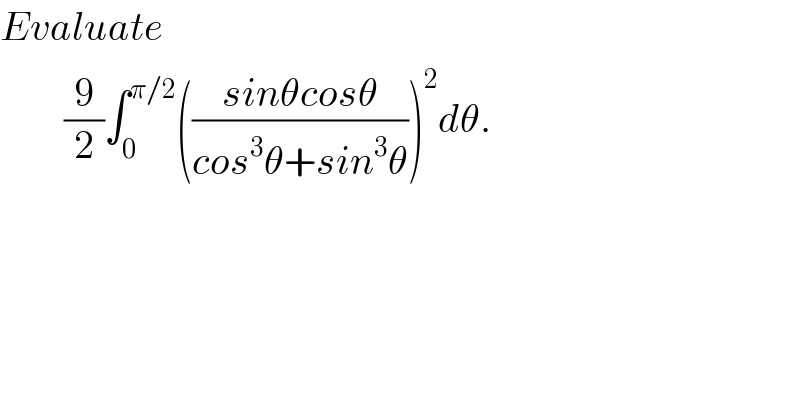
$${Evaluate} \\ $$$$\:\:\:\:\:\:\:\:\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\frac{{sin}\theta{cos}\theta}{{cos}^{\mathrm{3}} \theta+{sin}^{\mathrm{3}} \theta}\right)^{\mathrm{2}} {d}\theta. \\ $$
Answered by Filup last updated on 11/Nov/15
![=(9/2)∫_0 ^(π/2) ((sin^2 θcos^2 θ)/((cos^3 θ+sin^3 θ)^2 ))dθ =(9/2)∫_0 ^(π/2) ((sin^2 θcos^2 θ)/((cos^3 θ+sin^3 θ)^2 ))×((sec^6 θ)/(sec^6 θ))dθ =(9/2)∫_0 ^(π/2) (((sin^2 θ)/(cos^4 θ))/(cos^6 θsec^6 θ+2cos^3 θsin^3 θsec^6 θ+sin^6 θsec^6 θ))dθ =(9/2)∫_0 ^(π/2) ((tan^2 θsec^2 θ)/(1+2sin^3 θsec^3 θ+tan^6 θ))dθ =(9/2)∫_0 ^(π/2) ((tan^2 θsec^2 θ)/(1+2tan^3 θ+tan^6 θ))dθ =(9/2)∫_0 ^(π/2) ((tan^2 θsec^2 θ)/((1+tan^3 θ)^2 ))dθ u=tanθ du=sec^2 θdθ =(9/2)∫_0 ^(π/2) ((u^2 du)/((1+u^3 )^2 )) s=u^3 +1 ds=3u^2 du =(1/3)×(9/2)∫_0 ^(π/2) ((3u^2 du)/((1+u^3 )^2 )) =(9/6)∫_0 ^(π/2) (ds/s^2 ) =(3/2)∫_0 ^(π/2) (1/s^2 )ds =(3/2)[−(1/s)]_0 ^(π/2) =(3/2)[−(1/(u^3 +1))]_0 ^(π/2) =(3/2)[−(1/(tan^3 θ+1))]_0 ^(π/2) lim_(x→(π/2)^− ) tan(x)=+∞ =−(3/2)((1/(lim_(θ→(π/2)^− ) (tanθ)+1))−(1/(tan(0)+1))) =−(3/2)((1/∞)−(1/1))=−(3/2)(−1) =(3/2) ∴(9/2)∫_0 ^(π/2) (((sinθcosθ)/(cos^3 θ+sin^3 θ)))^2 dθ=(3/2)](https://www.tinkutara.com/question/Q2243.png)
$$=\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{sin}^{\mathrm{2}} \theta\mathrm{cos}^{\mathrm{2}} \theta}{\left(\mathrm{cos}^{\mathrm{3}} \theta+\mathrm{sin}^{\mathrm{3}} \theta\right)^{\mathrm{2}} }{d}\theta \\ $$$$ \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{sin}^{\mathrm{2}} \theta\mathrm{cos}^{\mathrm{2}} \theta}{\left(\mathrm{cos}^{\mathrm{3}} \theta+\mathrm{sin}^{\mathrm{3}} \theta\right)^{\mathrm{2}} }×\frac{\mathrm{sec}^{\mathrm{6}} \theta}{\mathrm{sec}^{\mathrm{6}} \theta}{d}\theta \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\frac{\mathrm{sin}^{\mathrm{2}} \theta}{\mathrm{cos}^{\mathrm{4}} \theta}}{\mathrm{cos}^{\mathrm{6}} \theta\mathrm{sec}^{\mathrm{6}} \theta+\mathrm{2cos}^{\mathrm{3}} \theta\mathrm{sin}^{\mathrm{3}} \theta\mathrm{sec}^{\mathrm{6}} \theta+\mathrm{sin}^{\mathrm{6}} \theta\mathrm{sec}^{\mathrm{6}} \theta}{d}\theta \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{tan}^{\mathrm{2}} \theta\mathrm{sec}^{\mathrm{2}} \theta}{\mathrm{1}+\mathrm{2sin}^{\mathrm{3}} \theta\mathrm{sec}^{\mathrm{3}} \theta+\mathrm{tan}^{\mathrm{6}} \theta}{d}\theta \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{tan}^{\mathrm{2}} \theta\mathrm{sec}^{\mathrm{2}} \theta}{\mathrm{1}+\mathrm{2tan}^{\mathrm{3}} \theta+\mathrm{tan}^{\mathrm{6}} \theta}{d}\theta \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{tan}^{\mathrm{2}} \theta\mathrm{sec}^{\mathrm{2}} \theta}{\left(\mathrm{1}+\mathrm{tan}^{\mathrm{3}} \theta\right)^{\mathrm{2}} }{d}\theta \\ $$$${u}=\mathrm{tan}\theta\:\:\:\:\:\:\:{du}=\mathrm{sec}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{u}^{\mathrm{2}} {du}}{\left(\mathrm{1}+{u}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$${s}={u}^{\mathrm{3}} +\mathrm{1}\:\:\:\:\:\:{ds}=\mathrm{3}{u}^{\mathrm{2}} {du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{3}{u}^{\mathrm{2}} {du}}{\left(\mathrm{1}+{u}^{\mathrm{3}} \right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{9}}{\mathrm{6}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{{ds}}{{s}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \frac{\mathrm{1}}{{s}^{\mathrm{2}} }{ds} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{{s}}\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{{u}^{\mathrm{3}} +\mathrm{1}}\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{\mathrm{tan}^{\mathrm{3}} \theta+\mathrm{1}}\right]_{\mathrm{0}} ^{\pi/\mathrm{2}} \\ $$$$\underset{{x}\rightarrow\left(\pi/\mathrm{2}\right)^{−} } {\mathrm{lim}}\:\mathrm{tan}\left({x}\right)=+\infty \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\underset{\theta\rightarrow\left(\pi/\mathrm{2}\right)^{−} } {\mathrm{lim}}\left(\mathrm{tan}\theta\right)+\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{tan}\left(\mathrm{0}\right)+\mathrm{1}}\right) \\ $$$$=−\frac{\mathrm{3}}{\mathrm{2}}\left(\frac{\mathrm{1}}{\infty}−\frac{\mathrm{1}}{\mathrm{1}}\right)=−\frac{\mathrm{3}}{\mathrm{2}}\left(−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$\therefore\frac{\mathrm{9}}{\mathrm{2}}\int_{\mathrm{0}} ^{\pi/\mathrm{2}} \left(\frac{\mathrm{sin}\theta\mathrm{cos}\theta}{\mathrm{cos}^{\mathrm{3}} \theta+\mathrm{sin}^{\mathrm{3}} \theta}\right)^{\mathrm{2}} {d}\theta=\frac{\mathrm{3}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by Filup last updated on 11/Nov/15
![Note: lim_(x→(π/2)^+ ) tan(x)=−∞ lim_(x→(π/2)^− ) tan(x)=+∞ The reasoning for my chioce of tan(π/2) is that for the intgral, x∈[0, π/2]. Thus as x→π/2, where x∈[0, π/2], f(x)→+∞.](https://www.tinkutara.com/question/Q2246.png)
$$\mathrm{Note}: \\ $$$$\underset{{x}\rightarrow\left(\pi/\mathrm{2}\right)^{+} } {\mathrm{lim}}\:\mathrm{tan}\left({x}\right)=−\infty \\ $$$$\underset{{x}\rightarrow\left(\pi/\mathrm{2}\right)^{−} } {\mathrm{lim}}\:\mathrm{tan}\left({x}\right)=+\infty \\ $$$$ \\ $$$$\mathrm{The}\:\mathrm{reasoning}\:\mathrm{for}\:\mathrm{my}\:\mathrm{chioce}\:\mathrm{of}\:\mathrm{tan}\left(\pi/\mathrm{2}\right) \\ $$$$\mathrm{is}\:\mathrm{that}\:\mathrm{for}\:\mathrm{the}\:\mathrm{intgral},\:{x}\in\left[\mathrm{0},\:\pi/\mathrm{2}\right]. \\ $$$$\mathrm{Thus}\:\mathrm{as}\:{x}\rightarrow\pi/\mathrm{2},\:\mathrm{where}\:{x}\in\left[\mathrm{0},\:\pi/\mathrm{2}\right], \\ $$$${f}\left({x}\right)\rightarrow+\infty. \\ $$
