Question Number 66016 by Rio Michael last updated on 07/Aug/19
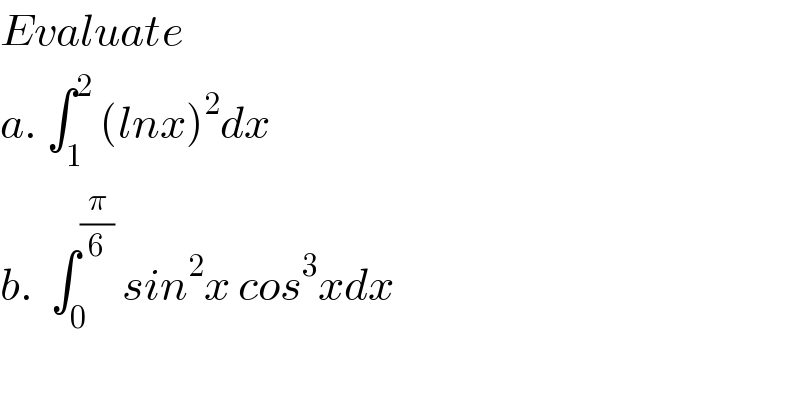
$${Evaluate}\:\:\: \\ $$$${a}.\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\left({lnx}\right)^{\mathrm{2}} {dx} \\ $$$${b}.\:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{3}} {xdx} \\ $$
Commented by Prithwish sen last updated on 07/Aug/19
![b.∫_0 ^(π/6) sin^2 x(1−sin^2 x)cosxdx now put sinx=u⇒cosx dx=du ∫_0 ^(1/2) u^2 (1−u^2 )du =∫_0 ^(1/2) (u^2 −u^4 )du =[(1/3)u^3 −(1/5)u^5 ]_0 ^(1/2) =(1/(24)) − (1/(160)) =((17)/(480)) please check.](https://www.tinkutara.com/question/Q66025.png)
$$\mathrm{b}.\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \mathrm{sin}^{\mathrm{2}} \mathrm{x}\left(\mathrm{1}−\mathrm{sin}^{\mathrm{2}} \mathrm{x}\right)\mathrm{cosxdx} \\ $$$$\mathrm{now}\:\mathrm{put}\:\mathrm{sinx}=\mathrm{u}\Rightarrow\mathrm{cosx}\:\mathrm{dx}=\mathrm{du} \\ $$$$\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{u}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{u}^{\mathrm{2}} \right)\mathrm{du}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \left(\mathrm{u}^{\mathrm{2}} −\mathrm{u}^{\mathrm{4}} \right)\mathrm{du}\:=\left[\frac{\mathrm{1}}{\mathrm{3}}\mathrm{u}^{\mathrm{3}} −\frac{\mathrm{1}}{\mathrm{5}}\mathrm{u}^{\mathrm{5}} \right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{24}}\:−\:\frac{\mathrm{1}}{\mathrm{160}}\:=\frac{\mathrm{17}}{\mathrm{480}}\:\:\mathrm{please}\:\mathrm{check}. \\ $$
Commented by Prithwish sen last updated on 07/Aug/19
![a.lnx = t⇒(dx/x) =dt⇒dx=e^t dt ∫_0 ^(ln2) t^2 e^t dt= [t^2 e^t −2te^t +2e^t ]_0 ^(ln2) =2(ln2)^2 −4ln2+2 please check.](https://www.tinkutara.com/question/Q66026.png)
$$\mathrm{a}.\mathrm{lnx}\:=\:\mathrm{t}\Rightarrow\frac{\mathrm{dx}}{\mathrm{x}}\:=\mathrm{dt}\Rightarrow\mathrm{dx}=\mathrm{e}^{\mathrm{t}} \mathrm{dt} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{ln2}} \mathrm{t}^{\mathrm{2}} \mathrm{e}^{\mathrm{t}} \mathrm{dt}=\:\left[\mathrm{t}^{\mathrm{2}} \mathrm{e}^{\mathrm{t}} −\mathrm{2te}^{\mathrm{t}} +\mathrm{2e}^{\mathrm{t}} \right]_{\mathrm{0}} ^{\mathrm{ln2}} =\mathrm{2}\left(\mathrm{ln2}\right)^{\mathrm{2}} −\mathrm{4ln2}+\mathrm{2} \\ $$$$\mathrm{please}\:\mathrm{check}. \\ $$
Commented by kaivan.ahmadi last updated on 07/Aug/19
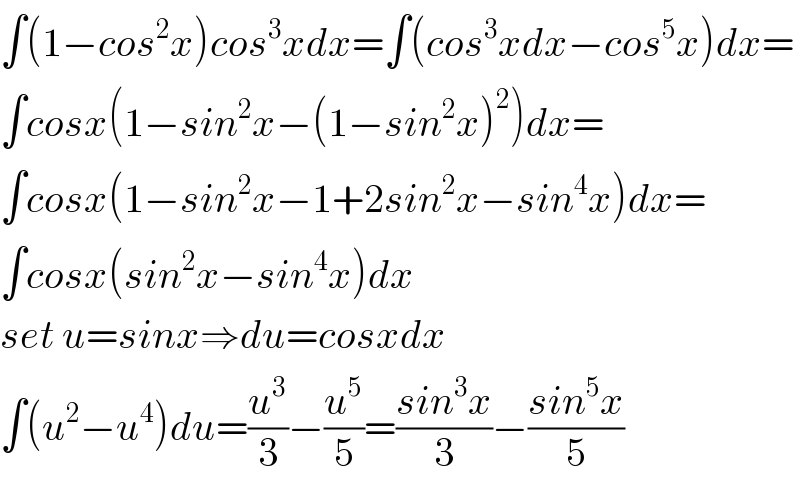
$$\int\left(\mathrm{1}−{cos}^{\mathrm{2}} {x}\right){cos}^{\mathrm{3}} {xdx}=\int\left({cos}^{\mathrm{3}} {xdx}−{cos}^{\mathrm{5}} {x}\right){dx}= \\ $$$$\int{cosx}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}−\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \right){dx}= \\ $$$$\int{cosx}\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}−\mathrm{1}+\mathrm{2}{sin}^{\mathrm{2}} {x}−{sin}^{\mathrm{4}} {x}\right){dx}= \\ $$$$\int{cosx}\left({sin}^{\mathrm{2}} {x}−{sin}^{\mathrm{4}} {x}\right){dx} \\ $$$${set}\:{u}={sinx}\Rightarrow{du}={cosxdx} \\ $$$$\int\left({u}^{\mathrm{2}} −{u}^{\mathrm{4}} \right){du}=\frac{{u}^{\mathrm{3}} }{\mathrm{3}}−\frac{{u}^{\mathrm{5}} }{\mathrm{5}}=\frac{{sin}^{\mathrm{3}} {x}}{\mathrm{3}}−\frac{{sin}^{\mathrm{5}} {x}}{\mathrm{5}} \\ $$
Commented by mathmax by abdo last updated on 07/Aug/19
![a) changement lnx =t give ∫_1 ^2 (lnx)^2 dx =∫_0 ^(ln(2)) t^2 e^t dt by parts ∫_0 ^(ln(2)) t^2 e^t dt =[t^2 e^t ]_0 ^(ln(2)) −∫_0 ^(ln(2)) 2t e^t dt =2(ln2)^2 −2 { [te^t ]_0 ^(ln(2)) −∫_0 ^(ln(2)) e^t dt} =2(ln(2))^2 −2{2ln(2)−(2−1)} =2(ln(2))^2 −4ln(2) +2](https://www.tinkutara.com/question/Q66030.png)
$$\left.{a}\right)\:{changement}\:{lnx}\:={t}\:{give}\:\int_{\mathrm{1}} ^{\mathrm{2}} \left({lnx}\right)^{\mathrm{2}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} {t}^{\mathrm{2}} {e}^{{t}} \:{dt}\:\:\:{by}\:{parts}\: \\ $$$$\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} {t}^{\mathrm{2}} {e}^{{t}} {dt}\:=\left[{t}^{\mathrm{2}} {e}^{{t}} \right]_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} −\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} \mathrm{2}{t}\:{e}^{{t}} {dt} \\ $$$$=\mathrm{2}\left({ln}\mathrm{2}\right)^{\mathrm{2}} \:−\mathrm{2}\:\left\{\:\:\left[{te}^{{t}} \right]_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} −\int_{\mathrm{0}} ^{{ln}\left(\mathrm{2}\right)} {e}^{{t}} {dt}\right\} \\ $$$$=\mathrm{2}\left({ln}\left(\mathrm{2}\right)\right)^{\mathrm{2}} −\mathrm{2}\left\{\mathrm{2}{ln}\left(\mathrm{2}\right)−\left(\mathrm{2}−\mathrm{1}\right)\right\} \\ $$$$=\mathrm{2}\left({ln}\left(\mathrm{2}\right)\right)^{\mathrm{2}} −\mathrm{4}{ln}\left(\mathrm{2}\right)\:+\mathrm{2}\: \\ $$
Commented by mathmax by abdo last updated on 07/Aug/19
![b) let I =∫_0 ^(π/6) sin^2 x cos^3 x ⇒I =∫_0 ^(π/6) (sinxcosx)^2 cosxdx =(1/4)∫_0 ^(π/6) sin^2 2x cosx dx =(1/4) ∫_0 ^(π/6) ((1−cos(4x))/2) cosx dx =(1/8) ∫_0 ^(π/6) (cosx−cos(4x)cosx)dx =(1/8) ∫_0 ^(π/6) cosxdx −(1/8) ∫_0 ^(π/6) cos(4x)cosxdx =(1/8).(1/2) −(1/(16)) ∫_0 ^(π/6) (cos(5x)+cos3x)dx =(1/(16))−(1/(16))[(1/5)sin(5x)+(1/3)sin(3x)]_0 ^(π/6) =(1/(16))−(1/(16)){(1/(10)) +(1/3)} =(1/(16))−(1/(160))−(1/(48)) =....](https://www.tinkutara.com/question/Q66031.png)
$$\left.{b}\right)\:{let}\:{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{3}} {x}\:\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\left({sinxcosx}\right)^{\mathrm{2}} {cosxdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:{sin}^{\mathrm{2}} \mathrm{2}{x}\:{cosx}\:{dx}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\frac{\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\:{cosx}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \left({cosx}−{cos}\left(\mathrm{4}{x}\right){cosx}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:{cosxdx}\:−\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:{cos}\left(\mathrm{4}{x}\right){cosxdx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}.\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{16}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \:\left({cos}\left(\mathrm{5}{x}\right)+{cos}\mathrm{3}{x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{16}}\left[\frac{\mathrm{1}}{\mathrm{5}}{sin}\left(\mathrm{5}{x}\right)+\frac{\mathrm{1}}{\mathrm{3}}{sin}\left(\mathrm{3}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{16}}\left\{\frac{\mathrm{1}}{\mathrm{10}}\:+\frac{\mathrm{1}}{\mathrm{3}}\right\}\:=\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mathrm{1}}{\mathrm{160}}−\frac{\mathrm{1}}{\mathrm{48}}\:=…. \\ $$
Commented by Rio Michael last updated on 07/Aug/19

$${Thanks}\:{sirs} \\ $$
Answered by Tanmay chaudhury last updated on 07/Aug/19
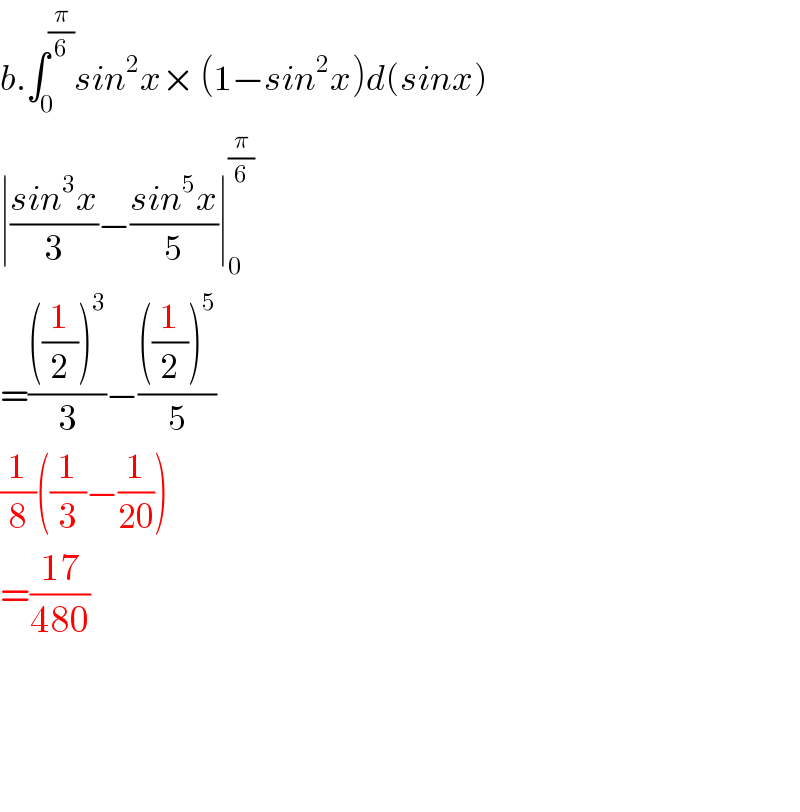
$${b}.\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} {sin}^{\mathrm{2}} {x}×\:\left(\mathrm{1}−{sin}^{\mathrm{2}} {x}\right){d}\left({sinx}\right) \\ $$$$\mid\frac{{sin}^{\mathrm{3}} {x}}{\mathrm{3}}−\frac{{sin}^{\mathrm{5}} {x}}{\mathrm{5}}\mid_{\mathrm{0}} ^{\frac{\pi}{\mathrm{6}}} \\ $$$$=\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{3}} }{\mathrm{3}}−\frac{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{5}} }{\mathrm{5}} \\ $$$$\frac{\mathrm{1}}{\mathrm{8}}\left(\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{20}}\right) \\ $$$$=\frac{\mathrm{17}}{\mathrm{480}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
