Question Number 75931 by Rio Michael last updated on 21/Dec/19

$${Evaluate} \\ $$$${a}.\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\sqrt[{\mathrm{3}}]{\frac{{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{27}{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$${b}.\:\:\underset{{x}\rightarrow−\infty} {\mathrm{lim}}\frac{{x}−\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${c}.\underset{{x}\rightarrow\infty} {\:\mathrm{lim}}\frac{{x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2}{x}−\mathrm{3}} \\ $$$${d}.\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{2}{x}\:+\:\mathrm{1}\:−\:\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}} \\ $$
Commented by turbo msup by abdo last updated on 21/Dec/19

$$\left.{a}\right){we}\:{have}\:{lim}_{{x}\rightarrow\infty} \:\:\frac{{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{27}{x}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{27}}\:\Rightarrow{lim}_{{x}\rightarrow\infty} \overset{\mathrm{3}} {\:}\sqrt{\frac{{x}^{\mathrm{2}} +\mathrm{3}}{\mathrm{27}{x}^{\mathrm{2}} −\mathrm{1}}} \\ $$$$=\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{\mathrm{27}}\right)}\:=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\left.{b}\right){lim}_{{x}\rightarrow−\infty} \:\:\:\frac{{x}−\mathrm{2}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$$={lim}_{{x}\rightarrow−\infty} \:\:\frac{{x}−\mathrm{2}}{\left.\:\sqrt{{x}^{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\right.}\right)} \\ $$$$={lim}_{{x}\rightarrow−\infty} \:\:\:\:\:\frac{{x}−\mathrm{2}}{\mid{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }}} \\ $$$$={lim}_{{x}\rightarrow−\infty} \:\:\:\frac{{x}}{−{x}}=−\mathrm{1} \\ $$
Commented by Rio Michael last updated on 21/Dec/19

$${thanks}\:{sir} \\ $$
Commented by turbo msup by abdo last updated on 21/Dec/19
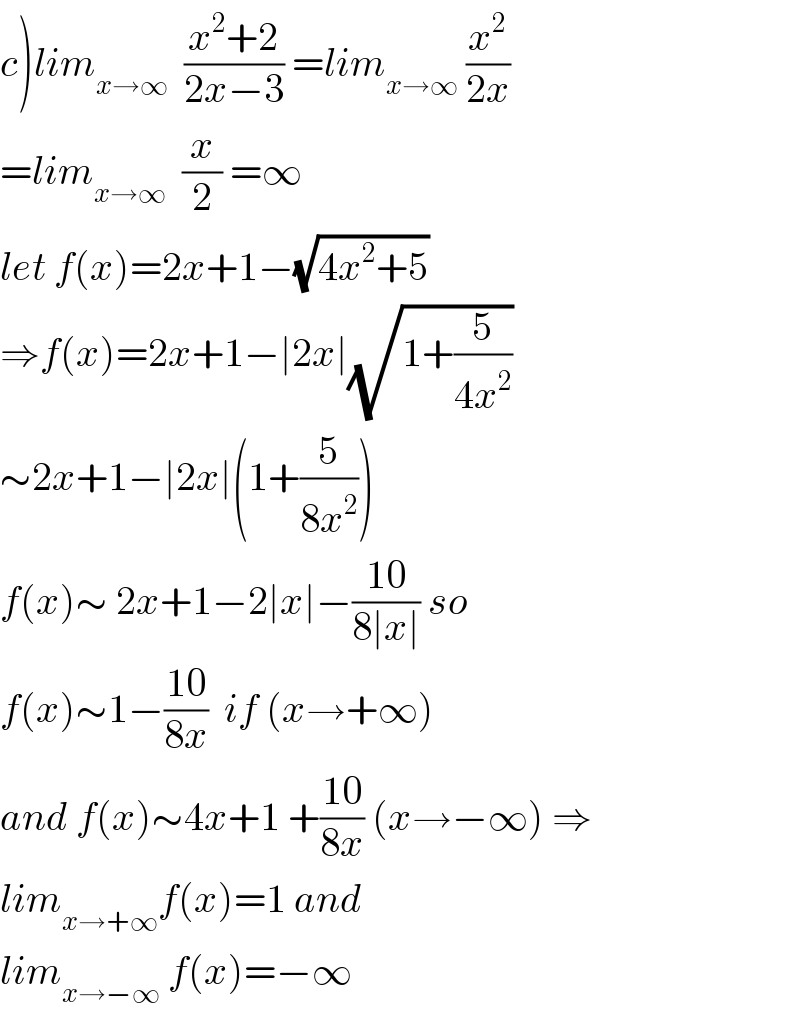
$$\left.{c}\right){lim}_{{x}\rightarrow\infty} \:\:\frac{{x}^{\mathrm{2}} +\mathrm{2}}{\mathrm{2}{x}−\mathrm{3}}\:={lim}_{{x}\rightarrow\infty} \:\frac{{x}^{\mathrm{2}} }{\mathrm{2}{x}} \\ $$$$={lim}_{{x}\rightarrow\infty} \:\:\frac{{x}}{\mathrm{2}}\:=\infty \\ $$$${let}\:{f}\left({x}\right)=\mathrm{2}{x}+\mathrm{1}−\sqrt{\mathrm{4}{x}^{\mathrm{2}} +\mathrm{5}} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{2}{x}+\mathrm{1}−\mid\mathrm{2}{x}\mid\sqrt{\mathrm{1}+\frac{\mathrm{5}}{\mathrm{4}{x}^{\mathrm{2}} }} \\ $$$$\sim\mathrm{2}{x}+\mathrm{1}−\mid\mathrm{2}{x}\mid\left(\mathrm{1}+\frac{\mathrm{5}}{\mathrm{8}{x}^{\mathrm{2}} }\right) \\ $$$${f}\left({x}\right)\sim\:\mathrm{2}{x}+\mathrm{1}−\mathrm{2}\mid{x}\mid−\frac{\mathrm{10}}{\mathrm{8}\mid{x}\mid}\:{so} \\ $$$${f}\left({x}\right)\sim\mathrm{1}−\frac{\mathrm{10}}{\mathrm{8}{x}}\:\:{if}\:\left({x}\rightarrow+\infty\right) \\ $$$${and}\:{f}\left({x}\right)\sim\mathrm{4}{x}+\mathrm{1}\:+\frac{\mathrm{10}}{\mathrm{8}{x}}\:\left({x}\rightarrow−\infty\right)\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow+\infty} {f}\left({x}\right)=\mathrm{1}\:{and} \\ $$$${lim}_{{x}\rightarrow−\infty} \:{f}\left({x}\right)=−\infty \\ $$
Commented by turbo msup by abdo last updated on 21/Dec/19

$${you}\:{are}\:{welcome}. \\ $$
