Menu Close

evaluate-cosx-x-2-1-2-dx-

Tinku Tara 0 Comments
Pin




Question Number 132090 by rs4089 last updated on 11/Feb/21
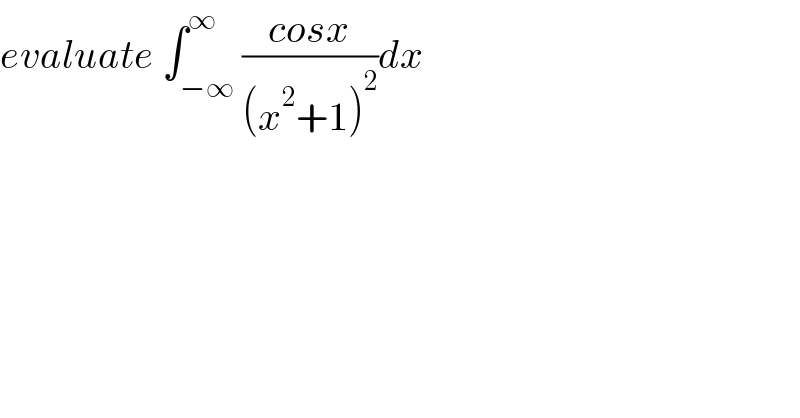
evaluate ∫_(−∞) ^∞ ((cosx)/((x^2 +1)^2 ))dx
$${evaluate}\:\int_{−\infty} ^{\infty} \frac{{cosx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$
Answered by Olaf last updated on 11/Feb/21
Ω = ∫_(−∞) ^(+∞) ((cosx)/((x^2 +1)^2 ))dx = 2∫_0 ^(+∞) ((cosx)/((x^2 +1)^2 ))dx Let I(t) = ∫_0 ^(+∞) ((cos(tx))/((x^2 +1)^2 ))dx L(I(t)) = ∫_0 ^(+∞) I(t)e^(−st) dt L(I(t)) = ∫_0 ^(+∞) ∫_0 ^(+∞) ((cos(tx))/((x^2 +1)^2 ))e^(−st) dxdt L(I(t)) = ∫_0 ^(+∞) ∫_0 ^(+∞) ((cos(tx))/((x^2 +1)^2 ))e^(−st) dtdx L(I(t)) = ∫_0 ^(+∞) (1/((x^2 +1)^2 ))L(cos(tx))dx L(I(t)) = ∫_0 ^(+∞) (1/((x^2 +1)^2 )).(s/(s^2 +x^2 ))dx L(I(t)) = (s/(s^2 −1))∫_0 ^(+∞) (dx/((x^2 +1)^2 )) −(s/((s^2 −1)^2 ))∫_0 ^(+∞) (dx/(x^2 +1))+(s/((s^2 −1)^2 ))∫_0 ^(+∞) (dx/(s^2 +x^2 )) L(I(t)) = (s/(s^2 −1)).(π/4)−(s/((s^2 −1)^2 )).(π/2)+(1/((s^2 −1)^2 )).(π/2) L(I(t)) = (π/4)[(s/(s^2 −1))−((2s)/((s^2 −1)^2 ))+(2/((s^2 −1)^2 ))] L(I(t)) = (π/4)[((s+2)/((s+1)^2 ))] L(I(t)) = (π/4)[(1/(s+1))+(1/((s+1)^2 ))] I(t) = (π/4)[e^(−t) Υ(t)+te^(−t) Υ(t)] Ω = 2I(t=1) = 2.(π/4)[(1/e)+1.(1/e)] Ω = (π/e) ...please verify sir...
$$\Omega\:=\:\int_{−\infty} ^{+\infty} \frac{\mathrm{cos}{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}\:=\:\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{cos}{x}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\mathrm{Let}\:\mathrm{I}\left({t}\right)\:=\:\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{cos}\left({tx}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$\mathcal{L}\left(\mathrm{I}\left({t}\right)\right)\:=\:\int_{\mathrm{0}} ^{+\infty} \mathrm{I}\left({t}\right){e}^{−{st}} {dt} \\ $$$$\mathcal{L}\left(\mathrm{I}\left({t}\right)\right)\:=\:\int_{\mathrm{0}} ^{+\infty} \int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{cos}\left({tx}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{e}^{−{st}} {dxdt} \\ $$$$\mathcal{L}\left(\mathrm{I}\left({t}\right)\right)\:=\:\int_{\mathrm{0}} ^{+\infty} \int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{cos}\left({tx}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{e}^{−{st}} {dtdx} \\ $$$$\mathcal{L}\left(\mathrm{I}\left({t}\right)\right)\:=\:\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\mathcal{L}\left(\mathrm{cos}\left({tx}\right)\right){dx} \\ $$$$\mathcal{L}\left(\mathrm{I}\left({t}\right)\right)\:=\:\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }.\frac{{s}}{{s}^{\mathrm{2}} +{x}^{\mathrm{2}} }{dx} \\ $$$$\mathcal{L}\left(\mathrm{I}\left({t}\right)\right)\:=\:\frac{{s}}{{s}^{\mathrm{2}} −\mathrm{1}}\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$−\frac{{s}}{\left({s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{{x}^{\mathrm{2}} +\mathrm{1}}+\frac{{s}}{\left({s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\int_{\mathrm{0}} ^{+\infty} \frac{{dx}}{{s}^{\mathrm{2}} +{x}^{\mathrm{2}} } \\ $$$$\mathcal{L}\left(\mathrm{I}\left({t}\right)\right)\:=\:\frac{{s}}{{s}^{\mathrm{2}} −\mathrm{1}}.\frac{\pi}{\mathrm{4}}−\frac{{s}}{\left({s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }.\frac{\pi}{\mathrm{2}}+\frac{\mathrm{1}}{\left({s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }.\frac{\pi}{\mathrm{2}} \\ $$$$\mathcal{L}\left(\mathrm{I}\left({t}\right)\right)\:=\:\frac{\pi}{\mathrm{4}}\left[\frac{{s}}{{s}^{\mathrm{2}} −\mathrm{1}}−\frac{\mathrm{2}{s}}{\left({s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{2}}{\left({s}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\mathcal{L}\left(\mathrm{I}\left({t}\right)\right)\:=\:\frac{\pi}{\mathrm{4}}\left[\frac{{s}+\mathrm{2}}{\left({s}+\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\mathcal{L}\left(\mathrm{I}\left({t}\right)\right)\:=\:\frac{\pi}{\mathrm{4}}\left[\frac{\mathrm{1}}{{s}+\mathrm{1}}+\frac{\mathrm{1}}{\left({s}+\mathrm{1}\right)^{\mathrm{2}} }\right] \\ $$$$\mathrm{I}\left({t}\right)\:=\:\frac{\pi}{\mathrm{4}}\left[{e}^{−{t}} \Upsilon\left({t}\right)+{te}^{−{t}} \Upsilon\left({t}\right)\right] \\ $$$$\Omega\:=\:\mathrm{2I}\left({t}=\mathrm{1}\right)\:=\:\mathrm{2}.\frac{\pi}{\mathrm{4}}\left[\frac{\mathrm{1}}{{e}}+\mathrm{1}.\frac{\mathrm{1}}{{e}}\right] \\ $$$$\Omega\:=\:\frac{\pi}{{e}} \\ $$$$…{please}\:{verify}\:{sir}… \\ $$$$ \\ $$
Commented by mnjuly1970 last updated on 11/Feb/21
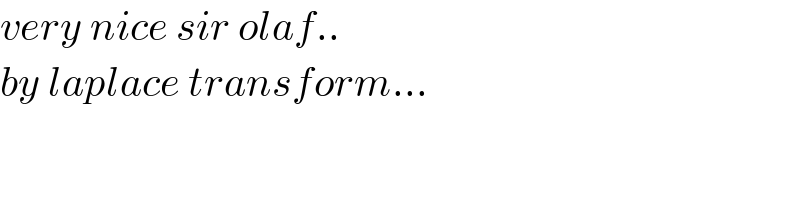
very nice sir olaf.. by laplace transform...
$${very}\:{nice}\:{sir}\:{olaf}.. \\ $$$${by}\:{laplace}\:{transform}… \\ $$
Answered by mnjuly1970 last updated on 11/Feb/21
another solution:: φ=∫_(−∞) ^( ∞) ((cos(x))/((x^2 +1)^2 ))dx =??? f(a)=∫_(−∞) ^( ∞) ((cos(x))/(x^2 +a^2 ))dx (a>0) =(2/a^2 )∫_0 ^( ∞) ((cos(x))/(((x/a))^2 +1))dx=^((x/a)=t) =(2/a)∫_0 ^( ∞) ((cos(at))/(t^2 +1))=(2/a).(π/2)e^(−a) =_(theorey) ^(residues) (π/a)e^(−a) ... f ′(a)=π(((−ae^(−a) −e^(−a) )/a^2 )) f ′(1)=−2πe^(−1) ......(1) on the other hand we know: f ′(a)=2∫_0 ^( ∞) ((−2acos(x))/((x^2 +a^2 )^2 ))dx f ′(1)=−4∫_0 ^( ∞) ((cos(x))/((x^2 +1)^2 ))dx=−2φ φ=((f ′(1))/(−2)) ......(2) from (1) and (2) ::∅=(π/e) ∴ ∫_(−∞) ^( ∞) ((cos(x))/((x^2 +1)^2 )) =(π/e)
$$\:\:\:\:\:{another}\:\:{solution}:: \\ $$$$\:\:\:\:\:\phi=\int_{−\infty} ^{\:\infty} \frac{{cos}\left({x}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}\:=??? \\ $$$$\:\:\:{f}\left({a}\right)=\int_{−\infty} ^{\:\infty} \frac{{cos}\left({x}\right)}{{x}^{\mathrm{2}} +{a}^{\mathrm{2}} }{dx}\:\:\left({a}>\mathrm{0}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}}{{a}^{\mathrm{2}} }\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left({x}\right)}{\left(\frac{{x}}{{a}}\right)^{\mathrm{2}} +\mathrm{1}}{dx}\overset{\frac{{x}}{{a}}={t}} {=} \\ $$$$\:\:\:\:\:\:\:=\frac{\mathrm{2}}{{a}}\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left({at}\right)}{{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{2}}{{a}}.\frac{\pi}{\mathrm{2}}{e}^{−{a}} \\ $$$$\:\:\:\:\:\:\:\:\underset{{theorey}} {\overset{{residues}} {=}}\:\frac{\pi}{{a}}{e}^{−{a}} \:… \\ $$$${f}\:'\left({a}\right)=\pi\left(\frac{−{ae}^{−{a}} −{e}^{−{a}} }{{a}^{\mathrm{2}} }\right) \\ $$$$\:\:{f}\:'\left(\mathrm{1}\right)=−\mathrm{2}\pi{e}^{−\mathrm{1}} ……\left(\mathrm{1}\right) \\ $$$$\:{on}\:{the}\:{other}\:{hand}\:\:{we}\:{know}: \\ $$$${f}\:'\left({a}\right)=\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{−\mathrm{2}{acos}\left({x}\right)}{\left({x}^{\mathrm{2}} +{a}^{\mathrm{2}} \right)^{\mathrm{2}} }{dx}\:\: \\ $$$$\:\:{f}\:'\left(\mathrm{1}\right)=−\mathrm{4}\int_{\mathrm{0}} ^{\:\infty} \frac{{cos}\left({x}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }{dx}=−\mathrm{2}\phi \\ $$$$\:\:\:\phi=\frac{{f}\:'\left(\mathrm{1}\right)}{−\mathrm{2}}\:……\left(\mathrm{2}\right) \\ $$$$\:\:\:{from}\:\:\left(\mathrm{1}\right)\:{and}\:\left(\mathrm{2}\right)\:::\emptyset=\frac{\pi}{{e}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\therefore\:\:\:\:\:\:\:\:\int_{−\infty} ^{\:\infty} \frac{{cos}\left({x}\right)}{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\pi}{{e}} \\ $$
Answered by mathmax by abdo last updated on 13/Feb/21
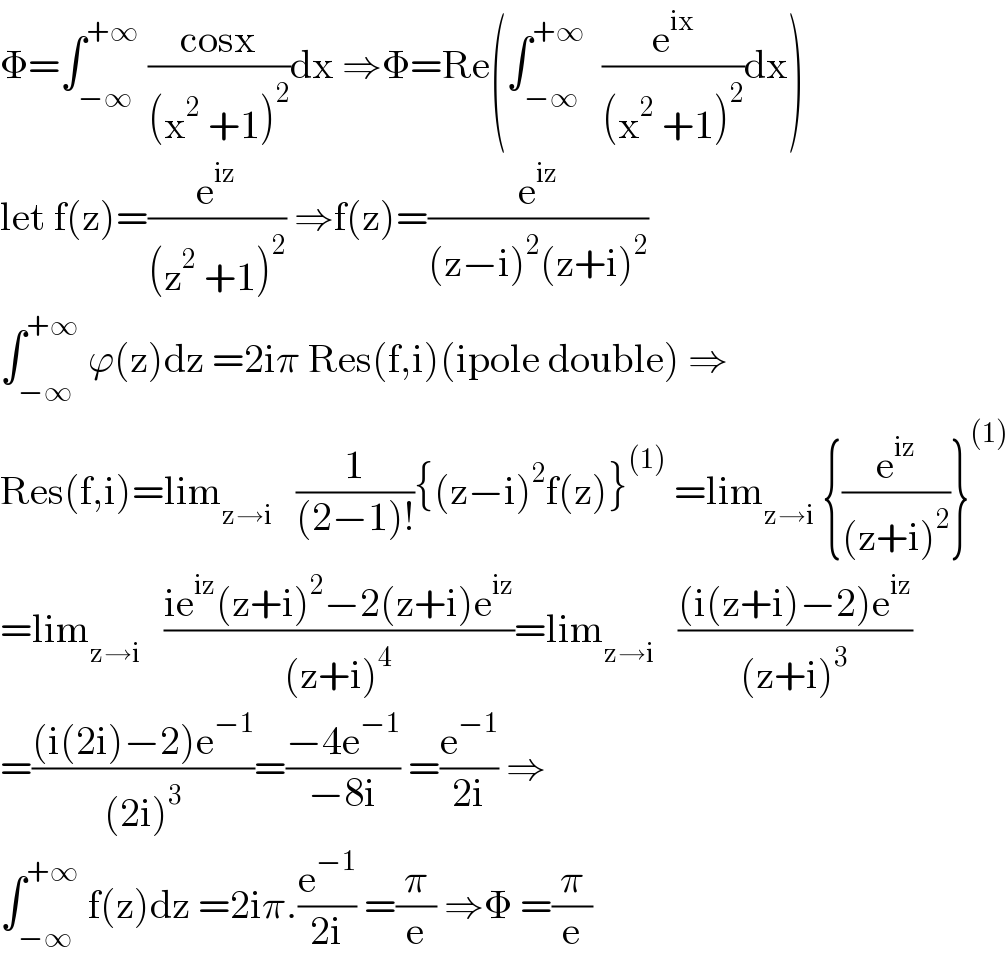
Φ=∫_(−∞) ^(+∞) ((cosx)/((x^2 +1)^2 ))dx ⇒Φ=Re(∫_(−∞) ^(+∞) (e^(ix) /((x^2 +1)^2 ))dx) let f(z)=(e^(iz) /((z^2 +1)^2 )) ⇒f(z)=(e^(iz) /((z−i)^2 (z+i)^2 )) ∫_(−∞) ^(+∞) ϕ(z)dz =2iπ Res(f,i)(ipole double) ⇒ Res(f,i)=lim_(z→i) (1/((2−1)!)){(z−i)^2 f(z)}^((1)) =lim_(z→i) {(e^(iz) /((z+i)^2 ))}^((1)) =lim_(z→i) ((ie^(iz) (z+i)^2 −2(z+i)e^(iz) )/((z+i)^4 ))=lim_(z→i) (((i(z+i)−2)e^(iz) )/((z+i)^3 )) =(((i(2i)−2)e^(−1) )/((2i)^3 ))=((−4e^(−1) )/(−8i)) =(e^(−1) /(2i)) ⇒ ∫_(−∞) ^(+∞) f(z)dz =2iπ.(e^(−1) /(2i)) =(π/e) ⇒Φ =(π/e)
$$\Phi=\int_{−\infty} ^{+\infty} \:\frac{\mathrm{cosx}}{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\:\Rightarrow\Phi=\mathrm{Re}\left(\int_{−\infty} ^{+\infty} \:\:\frac{\mathrm{e}^{\mathrm{ix}} }{\left(\mathrm{x}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\mathrm{dx}\right) \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}^{\mathrm{2}} \:+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{f}\left(\mathrm{z}\right)=\frac{\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }\: \\ $$$$\int_{−\infty} ^{+\infty} \:\varphi\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi\:\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)\left(\mathrm{ipole}\:\mathrm{double}\right)\:\Rightarrow \\ $$$$\mathrm{Res}\left(\mathrm{f},\mathrm{i}\right)=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\mathrm{1}}{\left(\mathrm{2}−\mathrm{1}\right)!}\left\{\left(\mathrm{z}−\mathrm{i}\right)^{\mathrm{2}} \mathrm{f}\left(\mathrm{z}\right)\right\}^{\left(\mathrm{1}\right)} \:=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\left\{\frac{\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} }\right\}^{\left(\mathrm{1}\right)} \\ $$$$=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\mathrm{ie}^{\mathrm{iz}} \left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{2}} −\mathrm{2}\left(\mathrm{z}+\mathrm{i}\right)\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{4}} }=\mathrm{lim}_{\mathrm{z}\rightarrow\mathrm{i}} \:\:\:\frac{\left(\mathrm{i}\left(\mathrm{z}+\mathrm{i}\right)−\mathrm{2}\right)\mathrm{e}^{\mathrm{iz}} }{\left(\mathrm{z}+\mathrm{i}\right)^{\mathrm{3}} } \\ $$$$=\frac{\left(\mathrm{i}\left(\mathrm{2i}\right)−\mathrm{2}\right)\mathrm{e}^{−\mathrm{1}} }{\left(\mathrm{2i}\right)^{\mathrm{3}} }=\frac{−\mathrm{4e}^{−\mathrm{1}} }{−\mathrm{8i}}\:=\frac{\mathrm{e}^{−\mathrm{1}} }{\mathrm{2i}}\:\Rightarrow \\ $$$$\int_{−\infty} ^{+\infty} \:\mathrm{f}\left(\mathrm{z}\right)\mathrm{dz}\:=\mathrm{2i}\pi.\frac{\mathrm{e}^{−\mathrm{1}} }{\mathrm{2i}}\:=\frac{\pi}{\mathrm{e}}\:\Rightarrow\Phi\:=\frac{\pi}{\mathrm{e}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *