Menu Close

evaluate-f-x-dx-where-f-x-e-x-x-0-1-x-0-lt-x-1-1-x-2-1-lt-x-2-5-2-lt-x-5-5-1-x-5-2-x-gt-5-

Tinku Tara
Pin




Question Number 216 by 123456 last updated on 25/Jan/15
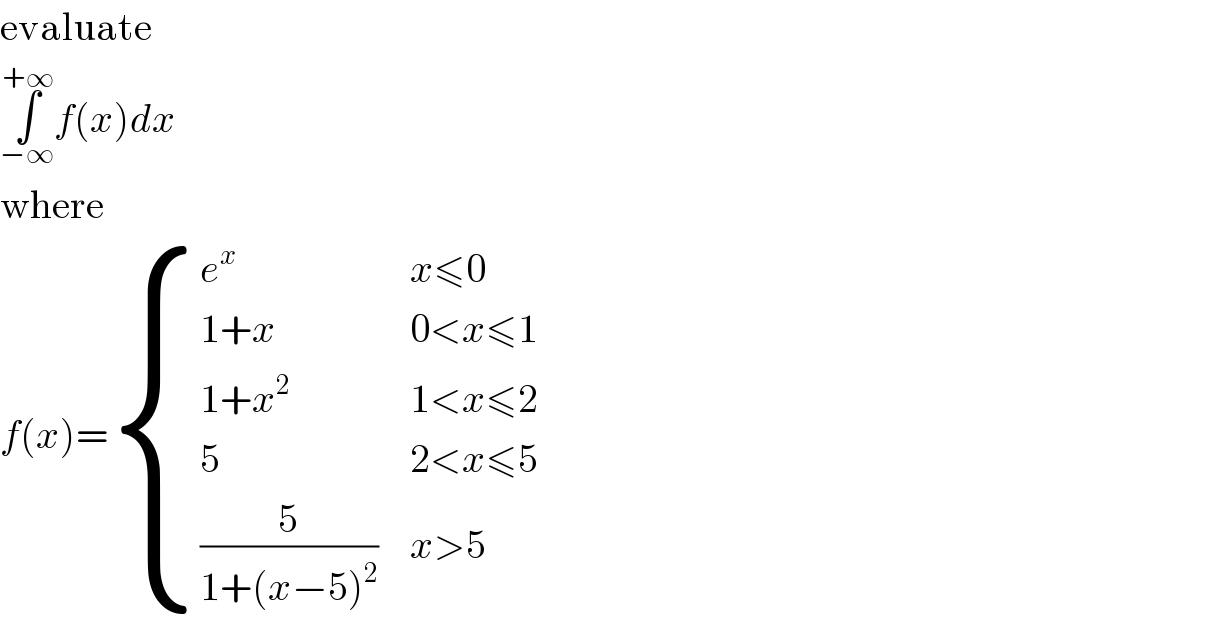
evaluate ∫_(−∞) ^(+∞) f(x)dx where f(x)= { (e^x ,(x≤0)),((1+x),(0<x≤1)),((1+x^2 ),(1<x≤2)),(5,(2<x≤5)),((5/(1+(x−5)^2 )),(x>5)) :}
$$\mathrm{evaluate} \\ $$$$\underset{−\infty} {\overset{+\infty} {\int}}{f}\left({x}\right){dx} \\ $$$$\mathrm{where} \\ $$$${f}\left({x}\right)=\begin{cases}{{e}^{{x}} }&{{x}\leqslant\mathrm{0}}\\{\mathrm{1}+{x}}&{\mathrm{0}<{x}\leqslant\mathrm{1}}\\{\mathrm{1}+{x}^{\mathrm{2}} }&{\mathrm{1}<{x}\leqslant\mathrm{2}}\\{\mathrm{5}}&{\mathrm{2}<{x}\leqslant\mathrm{5}}\\{\frac{\mathrm{5}}{\mathrm{1}+\left({x}−\mathrm{5}\right)^{\mathrm{2}} }}&{{x}>\mathrm{5}}\end{cases} \\ $$
Answered by prakash jain last updated on 16/Dec/14
=∫_(−∞) ^0 e^x dx+∫_0 ^1 (1+x)dx+∫_1 ^2 (1+x^2 )dx+∫_2 ^5 5dx +∫_5 ^∞ (5/(1+(x−5)^2 ))dx =1+[x+(x^2 /2)]_0 ^1 +[x+(x^3 /3)]_1 ^2 +[5x]_2 ^5 +[5tan^(−1) ((x−5)/1)]_5 ^∞ =1+(3/2)+[2+(8/3)−1−(1/3)]+[25−10]+[((5π)/2)] =(5/2)+((10)/3)+15+(π/2) =((15+20+90)/6)+(π/2)=((125)/2)+((5π)/2)
$$=\underset{−\infty} {\overset{\mathrm{0}} {\int}}{e}^{{x}} {dx}+\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\mathrm{1}+{x}\right){dx}+\underset{\mathrm{1}} {\overset{\mathrm{2}} {\int}}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}+\underset{\mathrm{2}} {\overset{\mathrm{5}} {\int}}\mathrm{5}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\underset{\mathrm{5}} {\overset{\infty} {\int}}\frac{\mathrm{5}}{\mathrm{1}+\left({x}−\mathrm{5}\right)^{\mathrm{2}} }{dx} \\ $$$$=\mathrm{1}+\left[{x}+\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} +\left[{x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}\right]_{\mathrm{1}} ^{\mathrm{2}} +\left[\mathrm{5}{x}\right]_{\mathrm{2}} ^{\mathrm{5}} +\left[\mathrm{5tan}^{−\mathrm{1}} \frac{{x}−\mathrm{5}}{\mathrm{1}}\right]_{\mathrm{5}} ^{\infty} \\ $$$$=\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}+\left[\mathrm{2}+\frac{\mathrm{8}}{\mathrm{3}}−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}\right]+\left[\mathrm{25}−\mathrm{10}\right]+\left[\frac{\mathrm{5}\pi}{\mathrm{2}}\right] \\ $$$$=\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{10}}{\mathrm{3}}+\mathrm{15}+\frac{\pi}{\mathrm{2}} \\ $$$$=\frac{\mathrm{15}+\mathrm{20}+\mathrm{90}}{\mathrm{6}}+\frac{\pi}{\mathrm{2}}=\frac{\mathrm{125}}{\mathrm{2}}+\frac{\mathrm{5}\pi}{\mathrm{2}} \\ $$

Pin