Question Number 143414 by Snail last updated on 14/Jun/21
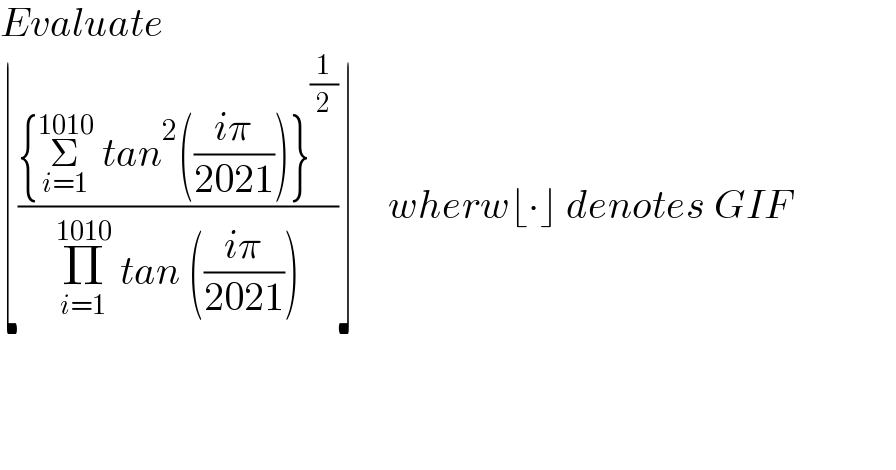
$${Evaluate}\: \\ $$$$\lfloor\frac{\left\{\underset{{i}=\mathrm{1}} {\overset{\mathrm{1010}} {\sum}}\:{tan}^{\mathrm{2}} \left(\frac{{i}\pi}{\mathrm{2021}}\right)\right\}^{\frac{\mathrm{1}}{\mathrm{2}}} }{\underset{{i}=\mathrm{1}} {\overset{\mathrm{1010}} {\prod}}\:{tan}\:\left(\frac{{i}\pi}{\mathrm{2021}}\right)}\rfloor\:\:\:\:{wherw}\lfloor\centerdot\rfloor\:{denotes}\:{GIF} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Olaf_Thorendsen last updated on 15/Jun/21
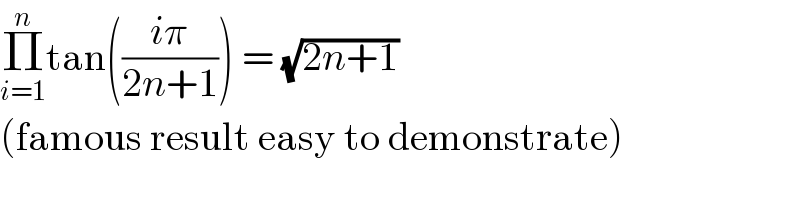
$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\prod}}\mathrm{tan}\left(\frac{{i}\pi}{\mathrm{2}{n}+\mathrm{1}}\right)\:=\:\sqrt{\mathrm{2}{n}+\mathrm{1}} \\ $$$$\left(\mathrm{famous}\:\mathrm{result}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{demonstrate}\right) \\ $$$$ \\ $$
Commented by Snail last updated on 15/Jun/21

$${What}\:{about}\:{the}\:{numerator}\:?…..{send}\:{me}\:{link}\:{of}\:{the}\:{result} \\ $$
