Question Number 6746 by Tawakalitu. last updated on 20/Jul/16
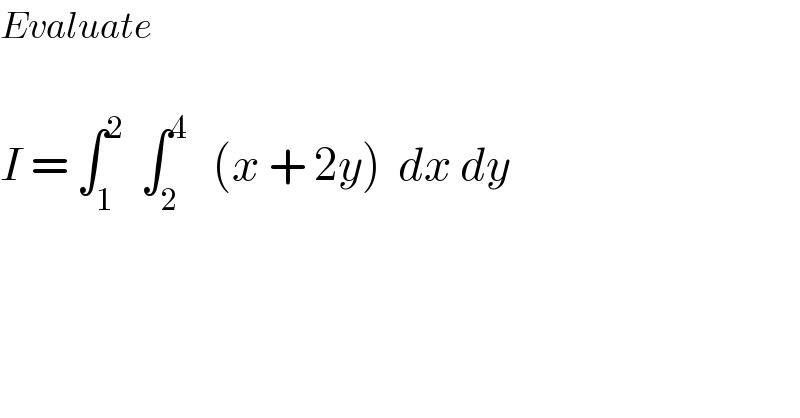
$${Evaluate}\: \\ $$$$ \\ $$$${I}\:=\:\int_{\mathrm{1}} ^{\mathrm{2}} \:\:\int_{\mathrm{2}} ^{\mathrm{4}} \:\:\:\left({x}\:+\:\mathrm{2}{y}\right)\:\:{dx}\:{dy}\: \\ $$
Answered by FilupSmith last updated on 20/Jul/16
![I=∫_1 ^( 2) [(1/2)x^2 +2xy]_2 ^4 dy I=∫_1 ^( 2) (6+4y)dy I=(6y+2y^2 )_1 ^2 I=(12+8)−(6+2) I=20−8 I=12](https://www.tinkutara.com/question/Q6747.png)
$${I}=\int_{\mathrm{1}} ^{\:\mathrm{2}} \left[\frac{\mathrm{1}}{\mathrm{2}}{x}^{\mathrm{2}} +\mathrm{2}{xy}\right]_{\mathrm{2}} ^{\mathrm{4}} {dy} \\ $$$${I}=\int_{\mathrm{1}} ^{\:\mathrm{2}} \left(\mathrm{6}+\mathrm{4}{y}\right){dy} \\ $$$${I}=\left(\mathrm{6}{y}+\mathrm{2}{y}^{\mathrm{2}} \right)_{\mathrm{1}} ^{\mathrm{2}} \\ $$$${I}=\left(\mathrm{12}+\mathrm{8}\right)−\left(\mathrm{6}+\mathrm{2}\right) \\ $$$${I}=\mathrm{20}−\mathrm{8} \\ $$$${I}=\mathrm{12} \\ $$
