Question Number 72688 by Rio Michael last updated on 31/Oct/19

$${Evaluate}\: \\ $$$$\:\underset{{t}\rightarrow\mathrm{9}} {\:{lim}}\frac{\mathrm{9}−{t}}{\mathrm{3}−\sqrt{{t}}\:} \\ $$
Answered by JDamian last updated on 01/Nov/19

$$\underset{{t}\rightarrow\mathrm{9}} {\mathrm{lim}}\left(\frac{\mathrm{9}−{t}}{\mathrm{3}−\sqrt{{t}}\:}×\frac{\mathrm{3}+\sqrt{{t}}}{\mathrm{3}+\sqrt{{t}}}\right)=\underset{{t}\rightarrow\mathrm{9}} {\mathrm{lim}}\frac{\left(\mathrm{9}−{t}\right)\left(\mathrm{3}+\sqrt{{t}}\right)}{\mathrm{9}−{t}}= \\ $$$$=\underset{{t}\rightarrow\mathrm{9}} {\mathrm{lim}}\:\left(\mathrm{3}+\sqrt{{t}}\right)=\mathrm{6} \\ $$
Commented by Rio Michael last updated on 31/Oct/19

$${thanks}\:{sir} \\ $$
Answered by malwaan last updated on 31/Oct/19
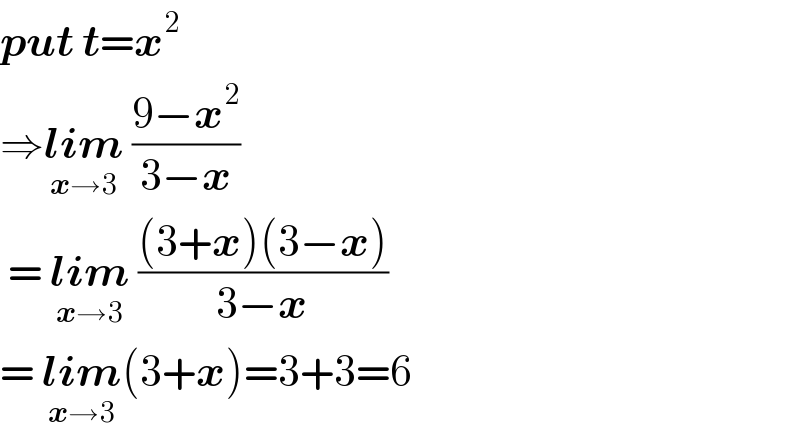
$$\boldsymbol{{put}}\:\boldsymbol{{t}}=\boldsymbol{{x}}^{\mathrm{2}\:} \: \\ $$$$\Rightarrow\underset{\boldsymbol{{x}}\rightarrow\mathrm{3}} {\boldsymbol{{lim}}}\:\frac{\mathrm{9}−\boldsymbol{{x}}^{\mathrm{2}} }{\mathrm{3}−\boldsymbol{{x}}} \\ $$$$\:=\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{3}} {\boldsymbol{{lim}}}\:\frac{\left(\mathrm{3}+\boldsymbol{{x}}\right)\left(\mathrm{3}−\boldsymbol{{x}}\right)}{\mathrm{3}−\boldsymbol{{x}}} \\ $$$$=\:\underset{\boldsymbol{{x}}\rightarrow\mathrm{3}} {\boldsymbol{{lim}}}\left(\mathrm{3}+\boldsymbol{{x}}\right)=\mathrm{3}+\mathrm{3}=\mathrm{6} \\ $$
Answered by petrochengula last updated on 01/Nov/19
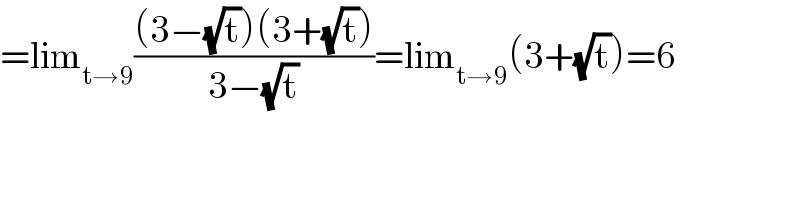
$$=\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{9}} \frac{\left(\mathrm{3}−\sqrt{\mathrm{t}}\right)\left(\mathrm{3}+\sqrt{\mathrm{t}}\right)}{\mathrm{3}−\sqrt{\mathrm{t}}}=\mathrm{lim}_{\mathrm{t}\rightarrow\mathrm{9}} \left(\mathrm{3}+\sqrt{\mathrm{t}}\right)=\mathrm{6} \\ $$
Commented by Rio Michael last updated on 01/Nov/19

$${thanks} \\ $$
