Question Number 77182 by jagoll last updated on 04/Jan/20
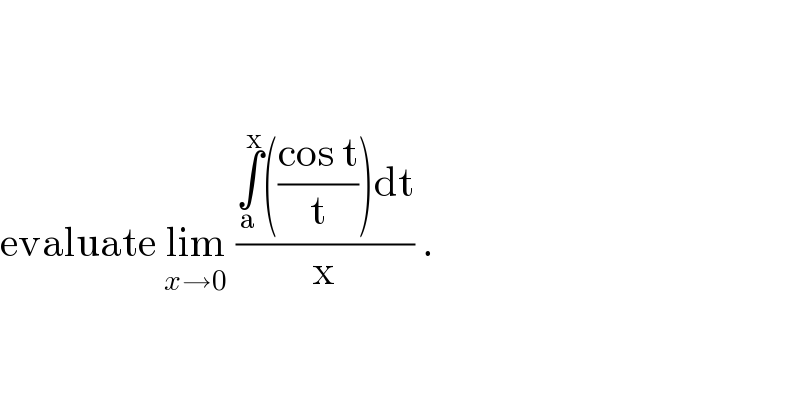
$$ \\ $$$$ \\ $$$$\mathrm{evaluate}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\underset{\mathrm{a}} {\overset{\mathrm{x}} {\int}}\left(\frac{\mathrm{cos}\:\mathrm{t}}{\mathrm{t}}\right)\mathrm{dt}}{\mathrm{x}}\:. \\ $$
Commented by mathmax by abdo last updated on 05/Jan/20

$${i}\:{think}\:{that}\:{a}=\mathrm{0}… \\ $$
Answered by john santu last updated on 04/Jan/20

$${suppose}\:{F}\left({t}\right)\:{is}\:{antiderivative} \\ $$$$\int\:\frac{\mathrm{cos}\:{t}}{{t}}\:{dt}\:{such}\:{that}\:\frac{{dF}\left({t}\right)}{{dt}}=\:\frac{\mathrm{cos}\:\left({t}\right)}{{t}}. \\ $$$${now}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{F}\left({t}\right)\underset{{a}} {\overset{{x}} {\mid}}}{{x}}=\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{F}\left({x}\right)−{F}\left({a}\right)}{{x}} \\ $$$${we}\:{assume}\:{that}\:{F}\left(\mathrm{0}\right)−{F}\left({a}\right)=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{F}'\left({x}\right)−{F}'\left({a}\right)}{\mathrm{1}}=\:{F}'\left(\mathrm{0}\right)−{F}'\left({a}\right) \\ $$$${but}\:{F}'\left(\mathrm{0}\right)\:=\:\frac{\mathrm{cos}\:\left(\mathrm{0}\right)}{\mathrm{0}}\:{undefined} \\ $$$${i}\:{think}\:{it}\:{problem}\:{error}. \\ $$$$ \\ $$
Commented by jagoll last updated on 04/Jan/20

$$\mathrm{thanks}\:\mathrm{sir}.\:\mathrm{i}\:\mathrm{will}\:\mathrm{check}\:\mathrm{my}\:\mathrm{question} \\ $$
