Question Number 8782 by uchechukwu okorie favour last updated on 27/Oct/16
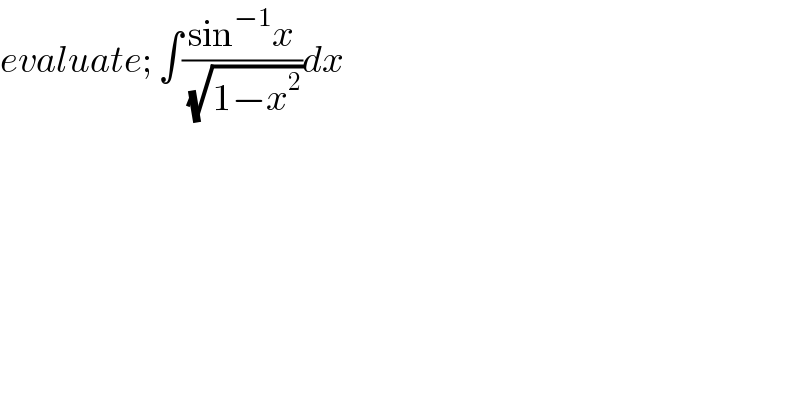
$${evaluate};\:\int\frac{\mathrm{sin}^{−\mathrm{1}} {x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$
Answered by prakash jain last updated on 27/Oct/16
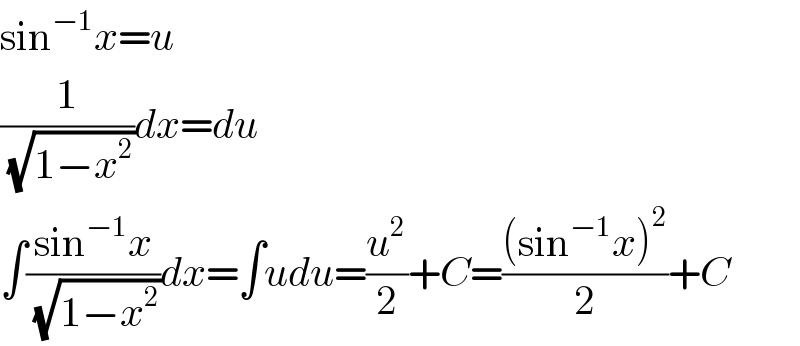
$$\mathrm{sin}^{−\mathrm{1}} {x}={u} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}={du} \\ $$$$\int\frac{\mathrm{sin}^{−\mathrm{1}} {x}}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}=\int{udu}=\frac{{u}^{\mathrm{2}} }{\mathrm{2}}+{C}=\frac{\left(\mathrm{sin}^{−\mathrm{1}} {x}\right)^{\mathrm{2}} }{\mathrm{2}}+{C} \\ $$
