Question Number 7189 by Tawakalitu. last updated on 15/Aug/16
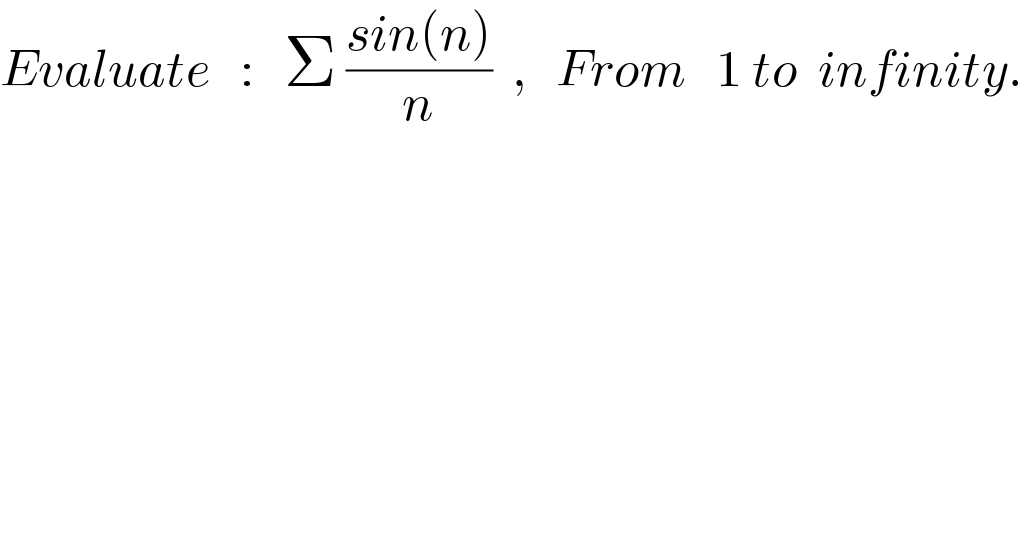
$${Evaluate}\:\:\::\:\:\:\Sigma\:\frac{{sin}\left({n}\right)}{{n}}\:\:,\:\:\:{From}\:\:\:\mathrm{1}\:{to}\:\:{infinity}. \\ $$
Commented by Yozzia last updated on 15/Aug/16
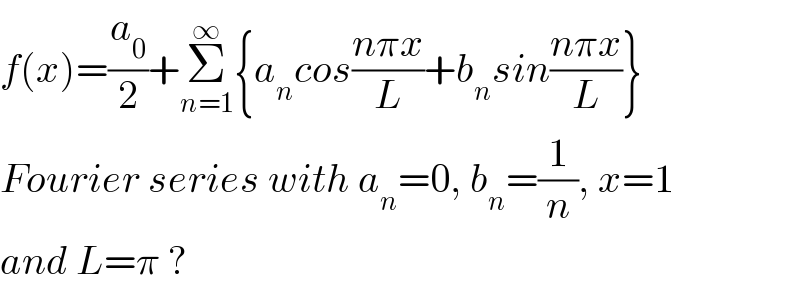
$${f}\left({x}\right)=\frac{{a}_{\mathrm{0}} }{\mathrm{2}}+\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left\{{a}_{{n}} {cos}\frac{{n}\pi{x}}{{L}}+{b}_{{n}} {sin}\frac{{n}\pi{x}}{{L}}\right\} \\ $$$${Fourier}\:{series}\:{with}\:{a}_{{n}} =\mathrm{0},\:{b}_{{n}} =\frac{\mathrm{1}}{{n}},\:{x}=\mathrm{1} \\ $$$${and}\:{L}=\pi\:? \\ $$
Commented by Tawakalitu. last updated on 15/Aug/16
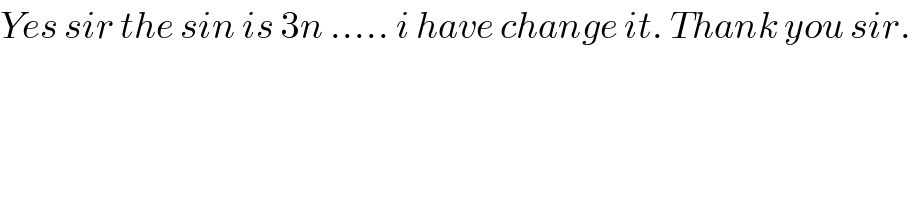
$${Yes}\:{sir}\:{the}\:{sin}\:{is}\:\mathrm{3}{n}\:…..\:{i}\:{have}\:{change}\:{it}.\:{Thank}\:{you}\:{sir}. \\ $$
