Evaluate-sinx-x-2-2x-2-dx-

Question Number 131957 by rs4089 last updated on 10/Feb/21

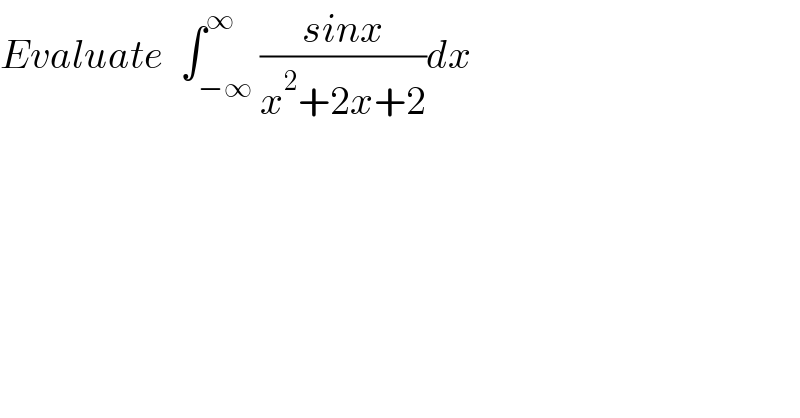
E v a l u a t e \int_{- \infty}^{\infty} \frac{s i n x}{x^{2} + 2 x + 2} d x

Answered by Dwaipayan Shikari last updated on 10/Feb/21

\int_{- \infty}^{\infty} \frac{s i n x}{{(x + 1)}^{2} + 1} x + 1 = u

= \int_{- \infty}^{\infty} \frac{s i n u c o s 1 - s i n 1 c o s u}{u^{2} + 1} d u

= c o s 1 \int_{- \infty}^{\infty} \frac{s i n u}{u^{2} + 1} - s i n 1 \int_{- \infty}^{\infty} \frac{c o s u}{u^{2} + 1} d u

= 0 - \frac{π}{e} s i n (1) = - \frac{π}{e} s i n (1)

Commented by mnjuly1970 last updated on 10/Feb/21

v e r y n i c e m r p a y a n \dots

Answered by mathmax by abdo last updated on 10/Feb/21

let f (λ) = \int_{- \infty}^{+ \infty} \frac{\sin (λ x)}{x^{2} + 2 x + 2} dx with λ > 0 \Rightarrow f (λ) = Im (\int_{- \infty}^{+ \infty} \frac{e^{i λ x}}{x^{2} + 2 x + 2} dx)

Φ (z) = \frac{e^{i λ z}}{z^{2} + 2 z + 2} we have z^{2} + 2 z + 2 = 0 \Rightarrow {(z + 1)}^{2} + 1 = 0 \Rightarrow

{(z + 1)}^{2} = - 1 \Rightarrow z + 1 = \bar{+} i \Rightarrow z = - 1 \bar{+} i si the poles of Φ are

z_{1} = - 1 + i and z_{2} = - 1 - i

\int_{R} Φ (z) dz = 2 i π Res (Φ, z_{1}) = 2 i π . \frac{e^{i λ z_{1}}}{2 i} = π e^{i λ (- 1 + i)}

= π e^{- i λ - λ} = π e^{- λ} {\cos (λ) - isin (λ)} \Rightarrow f (λ) = - π e^{- λ} \sin (λ)

\int_{- \infty}^{+ \infty} \frac{sinx}{x^{2} + 2 x + 2} dx = f (1) = - \frac{π}{e} \sin (1)