Menu Close

Evaluate-x-1-1-x-x-2-dx-

Tinku Tara
Pin




Question Number 50 by surabhi last updated on 25/Jan/15
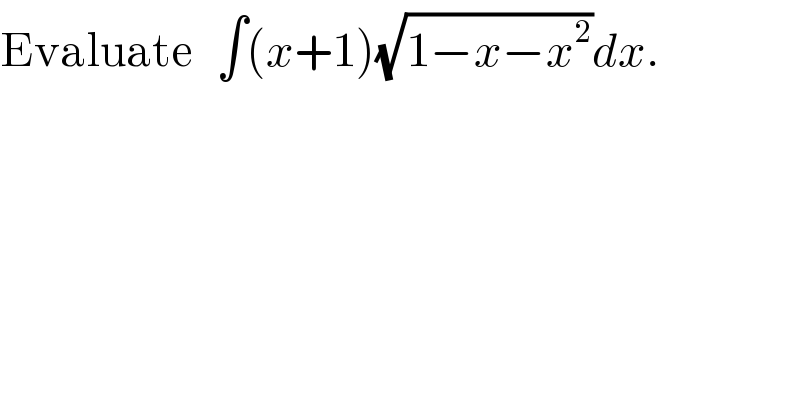
Evaluate ∫(x+1)(√(1−x−x^2 ))dx.
$$\mathrm{Evaluate}\:\:\:\int\left({x}+\mathrm{1}\right)\sqrt{\mathrm{1}−{x}−{x}^{\mathrm{2}} }{dx}. \\ $$
Commented by 123456 last updated on 13/Dec/14
tente?completar quadrados e fca uma substutuico
$$\mathrm{tente}?\mathrm{completar}\:\mathrm{quadrados}\:\mathrm{e}\:\mathrm{fca}\:\mathrm{uma}\:\mathrm{substutuico} \\ $$
Answered by 123456 last updated on 13/Dec/14
hint: −x^2 −x+1= −(x^2 +x)+1= −(x^2 +2×(1/2)×x)+1= −(x^2 +2×(1/2)×x+(1/4)−(1/4))+1= −(x+(1/2))^2 +(5/4)= ((−(2x+1)^2 +5)/4) from here you can use trigonometric substituition. for references the answer is at the coments, good luck :3
$$\mathrm{hint}: \\ $$$$−{x}^{\mathrm{2}} −{x}+\mathrm{1}= \\ $$$$−\left({x}^{\mathrm{2}} +{x}\right)+\mathrm{1}= \\ $$$$−\left({x}^{\mathrm{2}} +\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}×{x}\right)+\mathrm{1}= \\ $$$$−\left({x}^{\mathrm{2}} +\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}×{x}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}\right)+\mathrm{1}= \\ $$$$−\left({x}+\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{4}}= \\ $$$$\frac{−\left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} +\mathrm{5}}{\mathrm{4}} \\ $$$$\mathrm{from}\:\mathrm{here}\:\mathrm{you}\:\mathrm{can}\:\mathrm{use}\:\mathrm{trigonometric}\:\mathrm{substituition}. \\ $$$$\mathrm{for}\:\mathrm{references}\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{at}\:\mathrm{the}\:\mathrm{coments},\:\mathrm{good}\:\mathrm{luck}\::\mathrm{3} \\ $$
Commented by 123456 last updated on 13/Dec/14
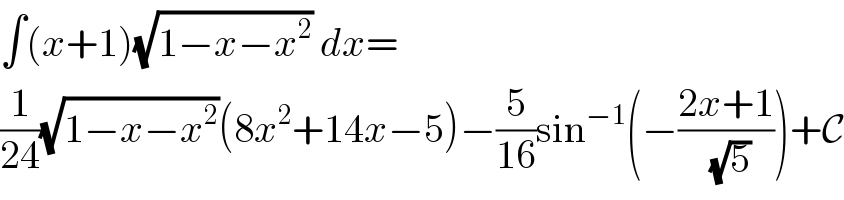
∫(x+1)(√(1−x−x^2 )) dx= (1/(24))(√(1−x−x^2 ))(8x^2 +14x−5)−(5/(16))sin^(−1) (−((2x+1)/( (√5))))+C
$$\int\left({x}+\mathrm{1}\right)\sqrt{\mathrm{1}−{x}−{x}^{\mathrm{2}} }\:{dx}= \\ $$$$\frac{\mathrm{1}}{\mathrm{24}}\sqrt{\mathrm{1}−{x}−{x}^{\mathrm{2}} }\left(\mathrm{8}{x}^{\mathrm{2}} +\mathrm{14}{x}−\mathrm{5}\right)−\frac{\mathrm{5}}{\mathrm{16}}\mathrm{sin}^{−\mathrm{1}} \left(−\frac{\mathrm{2}{x}+\mathrm{1}}{\:\sqrt{\mathrm{5}}}\right)+\mathcal{C} \\ $$

Pin