Question Number 144052 by physicstutes last updated on 21/Jun/21
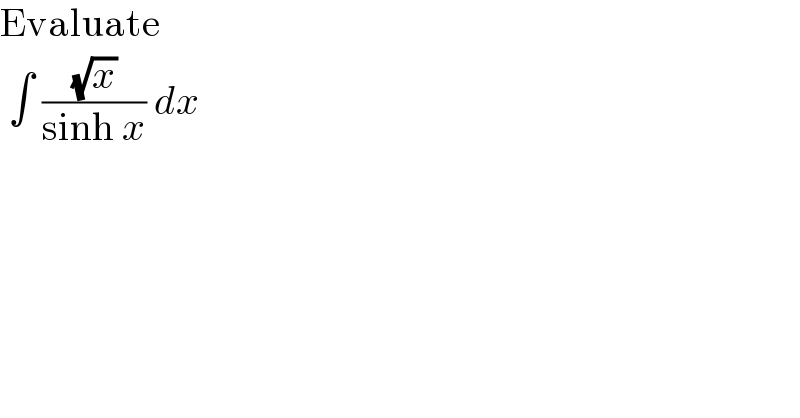
$$\mathrm{Evaluate}\: \\ $$$$\:\int\:\frac{\sqrt{{x}}}{\mathrm{sinh}\:{x}}\:{dx} \\ $$
Answered by mindispower last updated on 21/Jun/21

$${x}>\mathrm{0} \\ $$$$=\int\frac{\mathrm{2}{e}^{−{x}} \sqrt{{x}}{dx}}{\mathrm{1}−{e}^{−\mathrm{2}{x}} } \\ $$$$=\underset{{k}\geqslant\mathrm{0}} {\sum}\int\mathrm{2}{e}^{−\left(\mathrm{1}+\mathrm{2}{k}\right){x}} \sqrt{{x}}{dx} \\ $$$$=\mathrm{2}\underset{{k}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{2}{k}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }\int\sqrt{{x}}{e}^{−{x}} {dx} \\ $$$${recal}\:\Gamma\left({a},{x}\right)\:{incomplet}\:{Gamma}\:{function} \\ $$$$\Gamma\left({a},{x}\right)=\int_{{x}} ^{\infty} {t}^{{a}−\mathrm{1}} {e}^{−{t}} {dt} \\ $$$$\int\sqrt{{x}}{e}^{−{x}} {dx}=\int{x}^{\frac{\mathrm{3}}{\mathrm{2}}−\mathrm{1}} {e}^{−{x}} {dx}=−\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}},{x}\right)+{c} \\ $$$$\underset{{m}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{2}{k}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} }=\zeta\left(\frac{\mathrm{3}}{\mathrm{2}}\right)−\frac{\zeta\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\mathrm{2}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$${we}\:{get},\int\frac{\sqrt{{x}}}{{sh}\left({x}\right)}{dx}=−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{1}\right)\zeta\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}},{x}\right)+{c} \\ $$$${c}\in\mathbb{R} \\ $$
