Question Number 74622 by Raxreedoroid last updated on 27/Nov/19
![Expand 1+(2/3)∙(Σ_(k=1) ^(n−1) [cos(((2π)/3)x)]+2n−2)](https://www.tinkutara.com/question/Q74622.png)
$$\mathrm{Expand} \\ $$$$\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\centerdot\left(\underset{{k}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left[{cos}\left(\frac{\mathrm{2}\pi}{\mathrm{3}}{x}\right)\right]+\mathrm{2}{n}−\mathrm{2}\right) \\ $$
Commented by Raxreedoroid last updated on 28/Nov/19
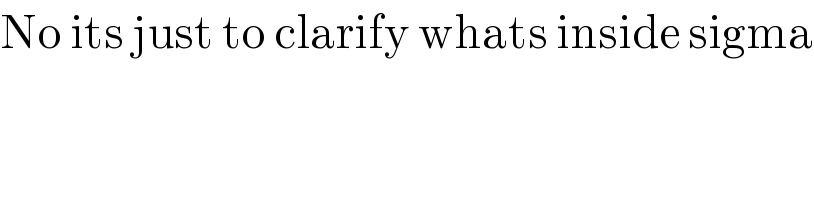
$$\mathrm{No}\:\mathrm{its}\:\mathrm{just}\:\mathrm{to}\:\mathrm{clarify}\:\mathrm{whats}\:\mathrm{inside}\:\mathrm{sigma} \\ $$
Commented by mind is power last updated on 28/Nov/19
![[cos(((2πk)/3))] is floor function ?](https://www.tinkutara.com/question/Q74672.png)
$$\left[\mathrm{cos}\left(\frac{\mathrm{2}\pi\mathrm{k}}{\mathrm{3}}\right)\right]\:\mathrm{is}\:\mathrm{floor}\:\mathrm{function}\:? \\ $$
Commented by JDamian last updated on 28/Nov/19
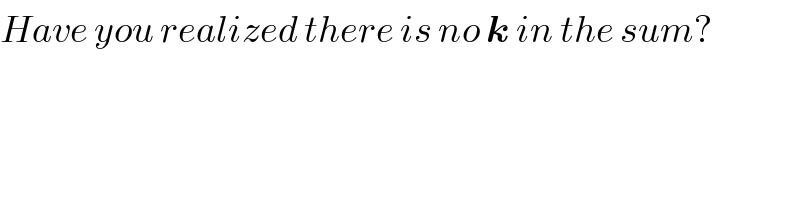
$${Have}\:{you}\:{realized}\:{there}\:{is}\:{no}\:\boldsymbol{{k}}\:{in}\:{the}\:{sum}? \\ $$
Commented by Raxreedoroid last updated on 01/Dec/19
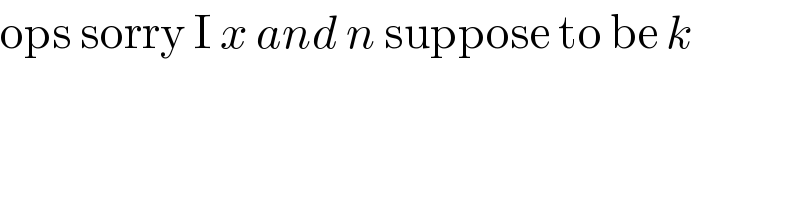
$$\mathrm{ops}\:\mathrm{sorry}\:\mathrm{I}\:{x}\:{and}\:{n}\:\mathrm{suppose}\:\mathrm{to}\:\mathrm{be}\:{k} \\ $$
