Menu Close

Explicit-f-x-1-lnt-x-2-t-2-2-dt-

Tinku Tara 0 Comments
Pin




Question Number 73293 by ~blr237~ last updated on 10/Nov/19
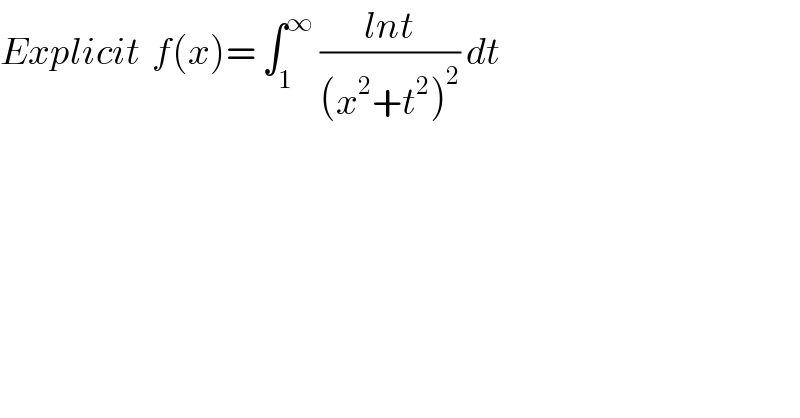
Explicit f(x)= ∫_1 ^∞ ((lnt)/((x^2 +t^2 )^2 )) dt
$${Explicit}\:\:{f}\left({x}\right)=\:\int_{\mathrm{1}} ^{\infty} \:\frac{{lnt}}{\left({x}^{\mathrm{2}} +{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:{dt}\: \\ $$
Commented by mathmax by abdo last updated on 10/Nov/19
let w(x)=∫_1 ^∞ ((lnt)/(x^2 +t^2 ))dt ⇒w(x)=_(t=(1/u)) −∫_0 ^1 ((−lnu)/(x^2 +(1/u^2 )))(−(du/u^2 )) =−∫_0 ^1 ((lnu)/(u^2 x^2 +1))du =_(ux=z) −∫_0 ^x ((ln((z/x)))/(z^2 +1))(dz/x) =−(1/x)∫_0 ^x ((lnz−lnx)/(z^2 +1))dz =−(1/x)∫_0 ^x ((lnz)/(z^2 +1))dz+((lnx)/x) arctanx w(x)=((lnx)/x)arctanx −(1/x)∫_0 ^x ((lnz)/(z^2 +1))dz and w^′ (x)= −∫_1 ^(+∞) ((2xlnt)/((x^2 +t^2 )^2 ))dt =−2xf(x) ⇒f(x)=−(1/(2x))w^′ (x) we have w^′ (x)=((1−lnx)/x^2 ) arctanx +((lnx)/(x(1+x^2 ))) +(1/x^2 ) ∫_0 ^x ((lnz)/(z^2 +1))dz −((lnx)/(x(x^2 +1))) ⇒ f(x)=−(1/(2x)){((1−lnx)/x^2 ) arctanx +(1/x^2 ) ∫_0 ^x ((lnz)/(z^2 +1))dz} =((lnx−1)/(2x^3 )) arctanx −(1/(2x^3 )) ∫_0 ^x ((lnz)/(z^2 +1))dz
$${let}\:{w}\left({x}\right)=\int_{\mathrm{1}} ^{\infty} \:\frac{{lnt}}{{x}^{\mathrm{2}} \:+{t}^{\mathrm{2}} }{dt}\:\Rightarrow{w}\left({x}\right)=_{{t}=\frac{\mathrm{1}}{{u}}} \:\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{−{lnu}}{{x}^{\mathrm{2}} \:+\frac{\mathrm{1}}{{u}^{\mathrm{2}} }}\left(−\frac{{du}}{{u}^{\mathrm{2}} }\right) \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{lnu}}{{u}^{\mathrm{2}} {x}^{\mathrm{2}} \:+\mathrm{1}}{du}\:=_{{ux}={z}} \:\:\:−\int_{\mathrm{0}} ^{{x}} \:\frac{{ln}\left(\frac{{z}}{{x}}\right)}{{z}^{\mathrm{2}} \:+\mathrm{1}}\frac{{dz}}{{x}} \\ $$$$=−\frac{\mathrm{1}}{{x}}\int_{\mathrm{0}} ^{{x}} \:\frac{{lnz}−{lnx}}{{z}^{\mathrm{2}} \:+\mathrm{1}}{dz}\:=−\frac{\mathrm{1}}{{x}}\int_{\mathrm{0}} ^{{x}} \:\frac{{lnz}}{{z}^{\mathrm{2}} \:+\mathrm{1}}{dz}+\frac{{lnx}}{{x}}\:{arctanx} \\ $$$${w}\left({x}\right)=\frac{{lnx}}{{x}}{arctanx}\:−\frac{\mathrm{1}}{{x}}\int_{\mathrm{0}} ^{{x}} \:\frac{{lnz}}{{z}^{\mathrm{2}} \:+\mathrm{1}}{dz}\:\:{and}\: \\ $$$${w}^{'} \left({x}\right)=\:−\int_{\mathrm{1}} ^{+\infty} \frac{\mathrm{2}{xlnt}}{\left({x}^{\mathrm{2}} \:+{t}^{\mathrm{2}} \right)^{\mathrm{2}} }{dt}\:=−\mathrm{2}{xf}\left({x}\right)\:\Rightarrow{f}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}{x}}{w}^{'} \left({x}\right)\:{we}\:{have} \\ $$$${w}^{'} \left({x}\right)=\frac{\mathrm{1}−{lnx}}{{x}^{\mathrm{2}} }\:{arctanx}\:+\frac{{lnx}}{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{{x}} \:\frac{{lnz}}{{z}^{\mathrm{2}} \:+\mathrm{1}}{dz}\:−\frac{{lnx}}{{x}\left({x}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${f}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{2}{x}}\left\{\frac{\mathrm{1}−{lnx}}{{x}^{\mathrm{2}} }\:{arctanx}\:+\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:\int_{\mathrm{0}} ^{{x}} \:\frac{{lnz}}{{z}^{\mathrm{2}} \:+\mathrm{1}}{dz}\right\} \\ $$$$=\frac{{lnx}−\mathrm{1}}{\mathrm{2}{x}^{\mathrm{3}} }\:{arctanx}\:−\frac{\mathrm{1}}{\mathrm{2}{x}^{\mathrm{3}} }\:\int_{\mathrm{0}} ^{{x}} \:\:\frac{{lnz}}{{z}^{\mathrm{2}} \:+\mathrm{1}}{dz} \\ $$
Commented by ~blr237~ last updated on 10/Nov/19
the first one
$${the}\:{first}\:\:{one} \\ $$
Answered by mind is power last updated on 10/Nov/19
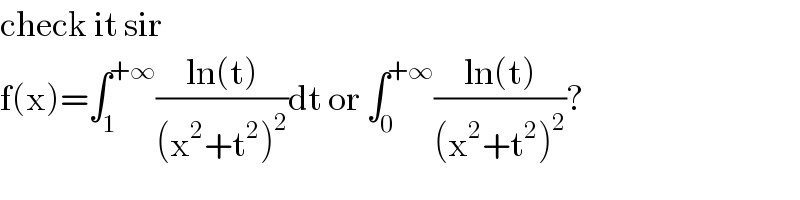
check it sir f(x)=∫_1 ^(+∞) ((ln(t))/((x^2 +t^2 )^2 ))dt or ∫_0 ^(+∞) ((ln(t))/((x^2 +t^2 )^2 ))?
$$\mathrm{check}\:\mathrm{it}\:\mathrm{sir}\: \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{1}} ^{+\infty} \frac{\mathrm{ln}\left(\mathrm{t}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\:\mathrm{or}\:\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{ln}\left(\mathrm{t}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }? \\ $$
Commented by ~blr237~ last updated on 10/Nov/19
the first one
$${the}\:{first}\:{one} \\ $$
Commented by ~blr237~ last updated on 10/Nov/19
the first one
$${the}\:{first}\:{one} \\ $$
Answered by mind is power last updated on 10/Nov/19
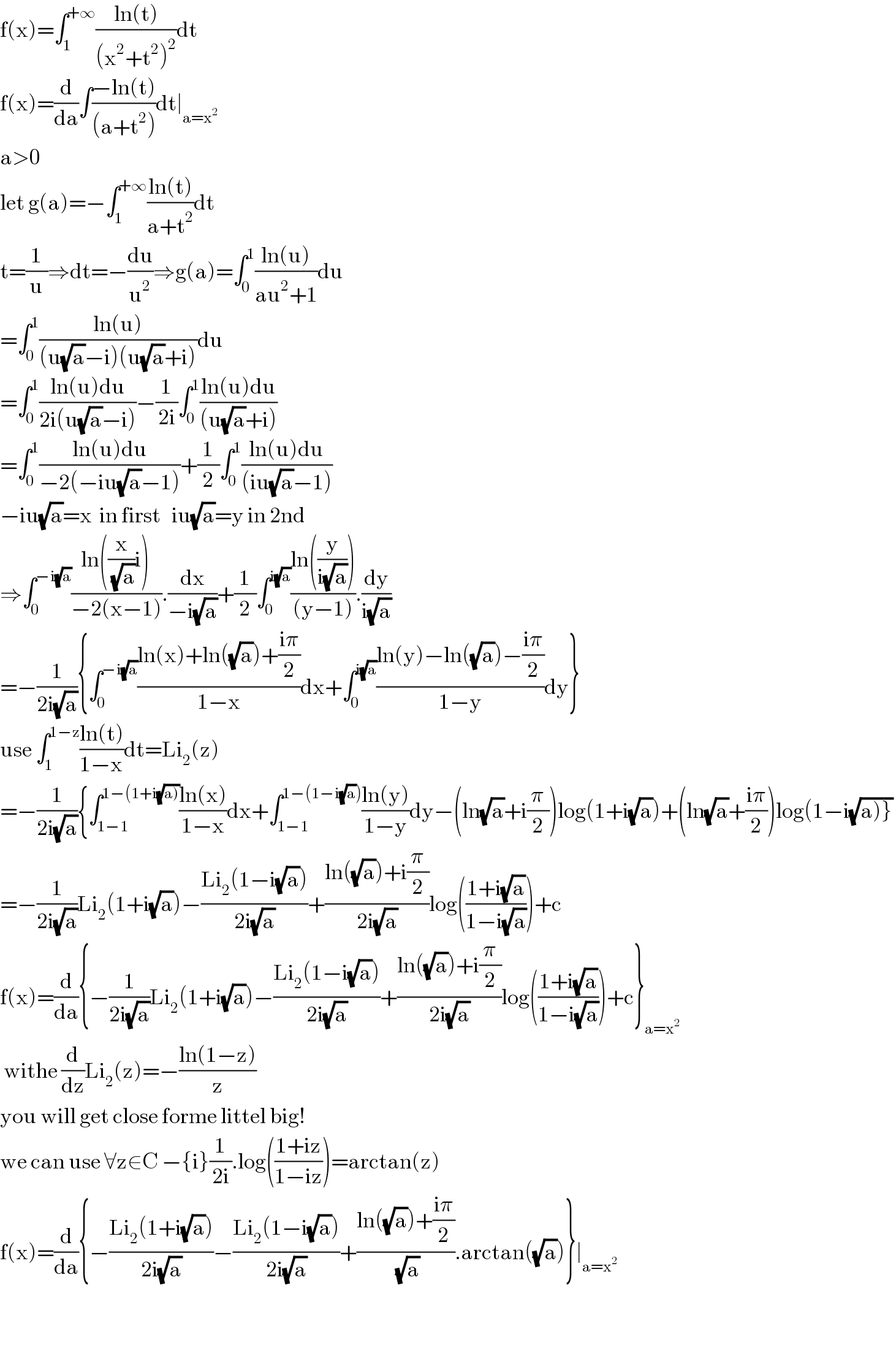
f(x)=∫_1 ^(+∞) ((ln(t))/((x^2 +t^2 )^2 ))dt f(x)=(d/da)∫((−ln(t))/((a+t^2 )))dt∣_(a=x^2 ) a>0 let g(a)=−∫_1 ^(+∞) ((ln(t))/(a+t^2 ))dt t=(1/u)⇒dt=−(du/u^2 )⇒g(a)=∫_0 ^1 ((ln(u))/(au^2 +1))du =∫_0 ^1 ((ln(u))/((u(√a)−i)(u(√a)+i)))du =∫_0 ^1 ((ln(u)du)/(2i(u(√a)−i)))−(1/(2i))∫_0 ^1 ((ln(u)du)/((u(√a)+i))) =∫_0 ^1 ((ln(u)du)/(−2(−iu(√a)−1)))+(1/2)∫_0 ^1 ((ln(u)du)/((iu(√a)−1))) −iu(√a)=x in first iu(√a)=y in 2nd ⇒∫_0 ^(−i(√a)) ((ln((x/( (√a)))i))/(−2(x−1))).(dx/(−i(√a)))+(1/2)∫_0 ^(i(√a)) ((ln((y/(i(√a)))))/((y−1))).(dy/(i(√a))) =−(1/(2i(√a))){∫_0 ^(−i(√a)) ((ln(x)+ln((√a))+((iπ)/2))/(1−x))dx+∫_0 ^(i(√a)) ((ln(y)−ln((√a))−((iπ)/2))/(1−y))dy} use ∫_1 ^(1−z) ((ln(t))/(1−x))dt=Li_2 (z) =−(1/(2i(√a))){∫_(1−1) ^(1−(1+i(√(a)))) ((ln(x))/(1−x))dx+∫_(1−1) ^(1−(1−i(√a))) ((ln(y))/(1−y))dy−(ln(√a)+i(π/2))log(1+i(√a))+(ln(√a)+((iπ)/2))log(1−i(√(a)})) =−(1/(2i(√a)))Li_2 (1+i(√a))−((Li_2 (1−i(√a)))/(2i(√a)))+((ln((√a))+i(π/2))/(2i(√a)))log(((1+i(√a))/(1−i(√a))))+c f(x)=(d/da){−(1/(2i(√a)))Li_2 (1+i(√a))−((Li_2 (1−i(√a)))/(2i(√a)))+((ln((√a))+i(π/2))/(2i(√a)))log(((1+i(√a))/(1−i(√a))))+c}_(a=x^2 ) withe (d/dz)Li_2 (z)=−((ln(1−z))/z) you will get close forme littel big! we can use ∀z∈C −{i}(1/(2i)).log(((1+iz)/(1−iz)))=arctan(z) f(x)=(d/da){−((Li_2 (1+i(√a)))/(2i(√a)))−((Li_2 (1−i(√a)))/(2i(√a)))+((ln((√a))+((iπ)/2))/( (√a))).arctan((√a))}∣_(a=x^2 )
$$\mathrm{f}\left(\mathrm{x}\right)=\int_{\mathrm{1}} ^{+\infty} \frac{\mathrm{ln}\left(\mathrm{t}\right)}{\left(\mathrm{x}^{\mathrm{2}} +\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{d}}{\mathrm{da}}\int\frac{−\mathrm{ln}\left(\mathrm{t}\right)}{\left(\mathrm{a}+\mathrm{t}^{\mathrm{2}} \right)}\mathrm{dt}\mid_{\mathrm{a}=\mathrm{x}^{\mathrm{2}} } \\ $$$$\mathrm{a}>\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{g}\left(\mathrm{a}\right)=−\int_{\mathrm{1}} ^{+\infty} \frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{a}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathrm{t}=\frac{\mathrm{1}}{\mathrm{u}}\Rightarrow\mathrm{dt}=−\frac{\mathrm{du}}{\mathrm{u}^{\mathrm{2}} }\Rightarrow\mathrm{g}\left(\mathrm{a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{u}\right)}{\mathrm{au}^{\mathrm{2}} +\mathrm{1}}\mathrm{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{u}\right)}{\left(\mathrm{u}\sqrt{\mathrm{a}}−\mathrm{i}\right)\left(\mathrm{u}\sqrt{\mathrm{a}}+\mathrm{i}\right)}\mathrm{du} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{u}\right)\mathrm{du}}{\mathrm{2i}\left(\mathrm{u}\sqrt{\mathrm{a}}−\mathrm{i}\right)}−\frac{\mathrm{1}}{\mathrm{2i}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{u}\right)\mathrm{du}}{\left(\mathrm{u}\sqrt{\mathrm{a}}+\mathrm{i}\right)} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{u}\right)\mathrm{du}}{−\mathrm{2}\left(−\mathrm{iu}\sqrt{\mathrm{a}}−\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left(\mathrm{u}\right)\mathrm{du}}{\left(\mathrm{iu}\sqrt{\mathrm{a}}−\mathrm{1}\right)} \\ $$$$−\mathrm{iu}\sqrt{\mathrm{a}}=\mathrm{x}\:\:\mathrm{in}\:\mathrm{first}\:\:\:\mathrm{iu}\sqrt{\mathrm{a}}=\mathrm{y}\:\mathrm{in}\:\mathrm{2nd} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{−\mathrm{i}\sqrt{\mathrm{a}}} \frac{\mathrm{ln}\left(\frac{\mathrm{x}}{\:\sqrt{\mathrm{a}}}\mathrm{i}\right)}{−\mathrm{2}\left(\mathrm{x}−\mathrm{1}\right)}.\frac{\mathrm{dx}}{−\mathrm{i}\sqrt{\mathrm{a}}}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{i}\sqrt{\mathrm{a}}} \frac{\mathrm{ln}\left(\frac{\mathrm{y}}{\mathrm{i}\sqrt{\mathrm{a}}}\right)}{\left(\mathrm{y}−\mathrm{1}\right)}.\frac{\mathrm{dy}}{\mathrm{i}\sqrt{\mathrm{a}}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2i}\sqrt{\mathrm{a}}}\left\{\int_{\mathrm{0}} ^{−\mathrm{i}\sqrt{\mathrm{a}}} \frac{\mathrm{ln}\left(\mathrm{x}\right)+\mathrm{ln}\left(\sqrt{\mathrm{a}}\right)+\frac{\mathrm{i}\pi}{\mathrm{2}}}{\mathrm{1}−\mathrm{x}}\mathrm{dx}+\int_{\mathrm{0}} ^{\mathrm{i}\sqrt{\mathrm{a}}} \frac{\mathrm{ln}\left(\mathrm{y}\right)−\mathrm{ln}\left(\sqrt{\mathrm{a}}\right)−\frac{\mathrm{i}\pi}{\mathrm{2}}}{\mathrm{1}−\mathrm{y}}\mathrm{dy}\right\} \\ $$$$\mathrm{use}\:\int_{\mathrm{1}} ^{\mathrm{1}−\mathrm{z}} \frac{\mathrm{ln}\left(\mathrm{t}\right)}{\mathrm{1}−\mathrm{x}}\mathrm{dt}=\mathrm{Li}_{\mathrm{2}} \left(\mathrm{z}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2i}\sqrt{\mathrm{a}}}\left\{\int_{\mathrm{1}−\mathrm{1}} ^{\mathrm{1}−\left(\mathrm{1}+\mathrm{i}\sqrt{\left.\mathrm{a}\right)}\right.} \frac{\mathrm{ln}\left(\mathrm{x}\right)}{\mathrm{1}−\mathrm{x}}\mathrm{dx}+\int_{\mathrm{1}−\mathrm{1}} ^{\mathrm{1}−\left(\mathrm{1}−\mathrm{i}\sqrt{\mathrm{a}}\right)} \frac{\mathrm{ln}\left(\mathrm{y}\right)}{\mathrm{1}−\mathrm{y}}\mathrm{dy}−\left(\mathrm{ln}\sqrt{\mathrm{a}}+\mathrm{i}\frac{\pi}{\mathrm{2}}\right)\mathrm{log}\left(\mathrm{1}+\mathrm{i}\sqrt{\mathrm{a}}\right)+\left(\mathrm{ln}\sqrt{\mathrm{a}}+\frac{\mathrm{i}\pi}{\mathrm{2}}\right)\mathrm{log}\left(\mathrm{1}−\mathrm{i}\sqrt{\left.\mathrm{a}\left.\right)\right\}}\right.\right. \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2i}\sqrt{\mathrm{a}}}\mathrm{Li}_{\mathrm{2}} \left(\mathrm{1}+\mathrm{i}\sqrt{\mathrm{a}}\right)−\frac{\mathrm{Li}_{\mathrm{2}} \left(\mathrm{1}−\mathrm{i}\sqrt{\mathrm{a}}\right)}{\mathrm{2i}\sqrt{\mathrm{a}}}+\frac{\mathrm{ln}\left(\sqrt{\mathrm{a}}\right)+\mathrm{i}\frac{\pi}{\mathrm{2}}}{\mathrm{2i}\sqrt{\mathrm{a}}}\mathrm{log}\left(\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{a}}}{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{a}}}\right)+\mathrm{c} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{d}}{\mathrm{da}}\left\{−\frac{\mathrm{1}}{\mathrm{2i}\sqrt{\mathrm{a}}}\mathrm{Li}_{\mathrm{2}} \left(\mathrm{1}+\mathrm{i}\sqrt{\mathrm{a}}\right)−\frac{\mathrm{Li}_{\mathrm{2}} \left(\mathrm{1}−\mathrm{i}\sqrt{\mathrm{a}}\right)}{\mathrm{2i}\sqrt{\mathrm{a}}}+\frac{\mathrm{ln}\left(\sqrt{\mathrm{a}}\right)+\mathrm{i}\frac{\pi}{\mathrm{2}}}{\mathrm{2i}\sqrt{\mathrm{a}}}\mathrm{log}\left(\frac{\mathrm{1}+\mathrm{i}\sqrt{\mathrm{a}}}{\mathrm{1}−\mathrm{i}\sqrt{\mathrm{a}}}\right)+\mathrm{c}\right\}_{\mathrm{a}=\mathrm{x}^{\mathrm{2}} } \\ $$$$\:\mathrm{withe}\:\frac{\mathrm{d}}{\mathrm{dz}}\mathrm{Li}_{\mathrm{2}} \left(\mathrm{z}\right)=−\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{z}\right)}{\mathrm{z}} \\ $$$$\mathrm{you}\:\mathrm{will}\:\mathrm{get}\:\mathrm{close}\:\mathrm{forme}\:\mathrm{littel}\:\mathrm{big}! \\ $$$$\mathrm{we}\:\mathrm{can}\:\mathrm{use}\:\forall\mathrm{z}\in\mathrm{C}\:−\left\{\mathrm{i}\right\}\frac{\mathrm{1}}{\mathrm{2i}}.\mathrm{log}\left(\frac{\mathrm{1}+\mathrm{iz}}{\mathrm{1}−\mathrm{iz}}\right)=\mathrm{arctan}\left(\mathrm{z}\right) \\ $$$$\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{d}}{\mathrm{da}}\left\{−\frac{\mathrm{Li}_{\mathrm{2}} \left(\mathrm{1}+\mathrm{i}\sqrt{\mathrm{a}}\right)}{\mathrm{2i}\sqrt{\mathrm{a}}}−\frac{\mathrm{Li}_{\mathrm{2}} \left(\mathrm{1}−\mathrm{i}\sqrt{\mathrm{a}}\right)}{\mathrm{2i}\sqrt{\mathrm{a}}}+\frac{\mathrm{ln}\left(\sqrt{\mathrm{a}}\right)+\frac{\mathrm{i}\pi}{\mathrm{2}}}{\:\sqrt{\mathrm{a}}}.\mathrm{arctan}\left(\sqrt{\mathrm{a}}\right)\right\}\mid_{\mathrm{a}=\mathrm{x}^{\mathrm{2}} } \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *