Question Number 1963 by 123456 last updated on 26/Oct/15
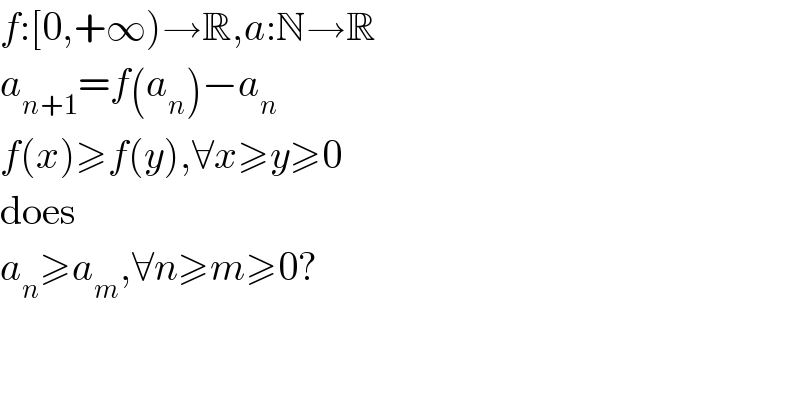
$${f}:\left[\mathrm{0},+\infty\right)\rightarrow\mathbb{R},{a}:\mathbb{N}\rightarrow\mathbb{R} \\ $$$${a}_{{n}+\mathrm{1}} ={f}\left({a}_{{n}} \right)−{a}_{{n}} \\ $$$${f}\left({x}\right)\geqslant{f}\left({y}\right),\forall{x}\geqslant{y}\geqslant\mathrm{0} \\ $$$$\mathrm{does} \\ $$$${a}_{{n}} \geqslant{a}_{{m}} ,\forall{n}\geqslant{m}\geqslant\mathrm{0}? \\ $$
Answered by prakash jain last updated on 26/Oct/15
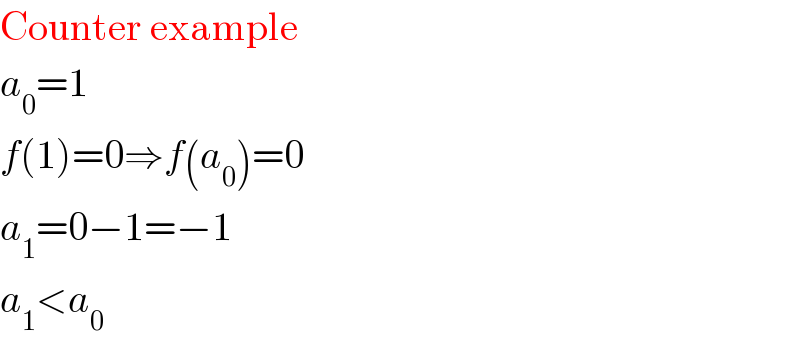
$$\mathrm{Counter}\:\mathrm{example} \\ $$$${a}_{\mathrm{0}} =\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0}\Rightarrow{f}\left({a}_{\mathrm{0}} \right)=\mathrm{0} \\ $$$${a}_{\mathrm{1}} =\mathrm{0}−\mathrm{1}=−\mathrm{1} \\ $$$${a}_{\mathrm{1}} <{a}_{\mathrm{0}} \\ $$
Commented by Rasheed Soomro last updated on 27/Oct/15

$${a}_{\mathrm{0}} =\mathrm{1}\:{Assumed}? \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0}\:{How}?\:{Is}\:{it}\:{also}\:{assumption}? \\ $$$${Question}\:{for}\:{sake}\:{of}\:{understanding}/{Knowledge}. \\ $$$${Not}\:{objection}. \\ $$
Commented by prakash jain last updated on 27/Oct/15

$$\mathrm{Values}\:\mathrm{assumed}\:\mathrm{which}\:\mathrm{satisfy}\:\mathrm{the}\:\mathrm{given} \\ $$$$\mathrm{conditions}\:\mathrm{in}\:\mathrm{question}\:\mathrm{to}\:\mathrm{create}\:\mathrm{a}\:\mathrm{counter} \\ $$$$\mathrm{example}. \\ $$$$\mathrm{We}\:\mathrm{can}\:\mathrm{also}\:\mathrm{use}\:{a}_{\mathrm{1}\:} \:\mathrm{and}\:{a}_{\mathrm{2}} \:\mathrm{and}\:\mathrm{use}\:\mathrm{differnt} \\ $$$$\mathrm{values}\:\mathrm{to}\:\mathrm{create}\:\mathrm{a}\:\mathrm{counter}\:\mathrm{example}\:\mathrm{as}\:\mathrm{long}\:\mathrm{as} \\ $$$${f}\left({a}_{\mathrm{1}} \right)−{a}_{\mathrm{1}} <{a}_{\mathrm{1}} \\ $$$${f}\left({a}_{\mathrm{1}} \right)<\mathrm{2}{a}_{\mathrm{1}} \\ $$
Commented by Rasheed Soomro last updated on 27/Oct/15

$$\mathcal{THANK}^{\mathcal{S}} \:! \\ $$
