Menu Close

f-0-x-1-f-1-x-x-f-n-1-x-x-f-n-x-f-n-x-n-N-

Tinku Tara
Pin




Question Number 356 by 123456 last updated on 25/Jan/15
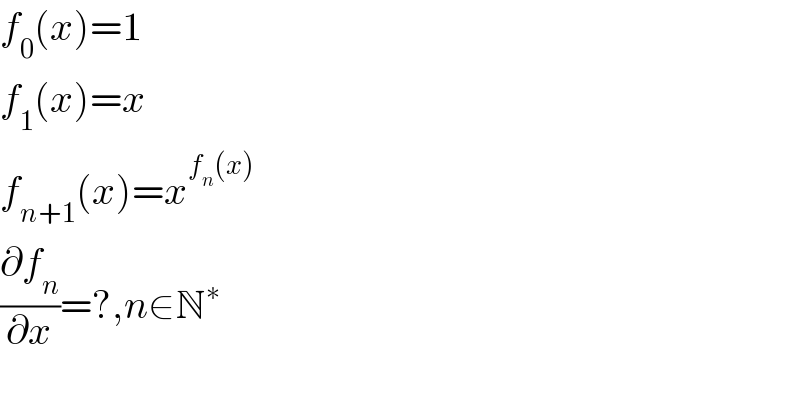
f_0 (x)=1 f_1 (x)=x f_(n+1) (x)=x^(f_n (x)) (∂f_n /∂x)=?,n∈N^∗
$${f}_{\mathrm{0}} \left({x}\right)=\mathrm{1} \\ $$$${f}_{\mathrm{1}} \left({x}\right)={x} \\ $$$${f}_{{n}+\mathrm{1}} \left({x}\right)={x}^{{f}_{{n}} \left({x}\right)} \\ $$$$\frac{\partial{f}_{{n}} }{\partial{x}}=?,{n}\in\mathbb{N}^{\ast} \\ $$
Answered by prakash jain last updated on 24/Dec/14
ln f_(n+1) (x)=f_n (x)ln x ((f ′_(n+1) (x))/(f_(n+1) (x)))=((f_n (x))/x)+ln x∙f ′_n (x) ((∂f_(n+1) (x))/(∂(x)))=f_(n+1) (x)[((f_n (x))/x)+((∂f_n (x))/∂x)∙ln x] ((∂f_0 (x))/∂x)=0 ((∂f_1 (x))/∂x)=1 ((∂f_2 (x))/(∂(x)))=x^x [(x/x)+ln x]=((x^x ∙x)/x)+((x^x .x)/x)ln x General Term for n≥2 ((∂f_n (x))/∂x)=((f_(n−1) (x)∙f_n (x))/x)+f_n (x){Σ_(j=1) ^(n−1) [(1/x)∙Π_(i=1) ^(n−1) f_i (x)(ln x)^i ]}
$$\mathrm{ln}\:{f}_{{n}+\mathrm{1}} \left({x}\right)={f}_{{n}} \left({x}\right)\mathrm{ln}\:{x} \\ $$$$\frac{{f}\:'_{{n}+\mathrm{1}} \left({x}\right)}{{f}_{{n}+\mathrm{1}} \left({x}\right)}=\frac{{f}_{{n}} \left({x}\right)}{{x}}+\mathrm{ln}\:{x}\centerdot{f}\:'_{{n}} \left({x}\right) \\ $$$$\frac{\partial{f}_{{n}+\mathrm{1}} \left({x}\right)}{\partial\left({x}\right)}={f}_{{n}+\mathrm{1}} \left({x}\right)\left[\frac{{f}_{{n}} \left({x}\right)}{{x}}+\frac{\partial{f}_{{n}} \left({x}\right)}{\partial{x}}\centerdot\mathrm{ln}\:{x}\right] \\ $$$$\frac{\partial{f}_{\mathrm{0}} \left({x}\right)}{\partial{x}}=\mathrm{0} \\ $$$$\frac{\partial{f}_{\mathrm{1}} \left({x}\right)}{\partial{x}}=\mathrm{1} \\ $$$$\frac{\partial{f}_{\mathrm{2}} \left({x}\right)}{\partial\left({x}\right)}={x}^{{x}} \left[\frac{{x}}{{x}}+\mathrm{ln}\:{x}\right]=\frac{{x}^{{x}} \centerdot{x}}{{x}}+\frac{{x}^{{x}} .{x}}{{x}}\mathrm{ln}\:{x} \\ $$$$\mathrm{General}\:\mathrm{Term}\:\mathrm{for}\:{n}\geqslant\mathrm{2} \\ $$$$\frac{\partial{f}_{{n}} \left({x}\right)}{\partial{x}}=\frac{{f}_{{n}−\mathrm{1}} \left({x}\right)\centerdot{f}_{{n}} \left({x}\right)}{{x}}+{f}_{{n}} \left({x}\right)\left\{\underset{{j}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\sum}}\left[\frac{\mathrm{1}}{{x}}\centerdot\underset{{i}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}{f}_{{i}} \left({x}\right)\left(\mathrm{ln}\:{x}\right)^{{i}} \right]\right\} \\ $$

Pin