Question Number 5978 by FilupSmith last updated on 08/Jun/16
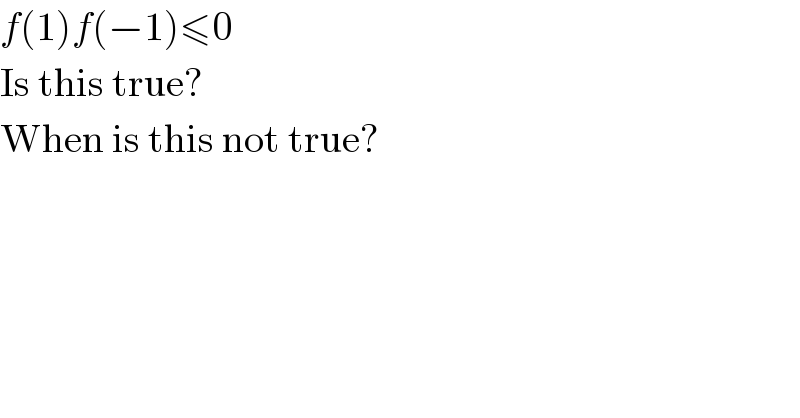
$${f}\left(\mathrm{1}\right){f}\left(−\mathrm{1}\right)\leqslant\mathrm{0} \\ $$$$\mathrm{Is}\:\mathrm{this}\:\mathrm{true}? \\ $$$$\mathrm{When}\:\mathrm{is}\:\mathrm{this}\:\mathrm{not}\:\mathrm{true}? \\ $$
Commented by Yozzii last updated on 09/Jun/16
![If x∈R, f(x)∈R is odd ⇒f(x)f(−x)=−(f(x))^2 ≤0 Equality arises if the value of x chosen is the root of f(x)=0. The set U of all functions consist of those that are odd (O), even (E) or neither odd nor even (N). ⇒U=O∪E∪N. An example of f(x)∈N is f: x∣→x−cosx. ∴ f(x)=x−cosx f(−x)=−x−cosx≠f(x) and f(−x)≠−f(x). Perhaps one general way to construct some members of N includes the form f(x)=Σ_(i=1) ^n g_i (x) where at least one function g_i (x) is different in parity from the others for some i∈[1,n] where n≥2.](https://www.tinkutara.com/question/Q6013.png)
$${If}\:{x}\in\mathbb{R},\:{f}\left({x}\right)\in\mathbb{R}\:{is}\:{odd}\:\Rightarrow{f}\left({x}\right){f}\left(−{x}\right)=−\left({f}\left({x}\right)\right)^{\mathrm{2}} \leqslant\mathrm{0} \\ $$$${Equality}\:{arises}\:{if}\:{the}\:{value}\:{of}\:{x}\:{chosen} \\ $$$${is}\:{the}\:{root}\:{of}\:{f}\left({x}\right)=\mathrm{0}. \\ $$$${The}\:{set}\:{U}\:{of}\:{all}\:{functions}\:{consist} \\ $$$${of}\:{those}\:{that}\:{are}\:{odd}\:\left({O}\right),\:{even}\:\left({E}\right)\:{or} \\ $$$${neither}\:{odd}\:{nor}\:{even}\:\left({N}\right). \\ $$$$\Rightarrow{U}={O}\cup{E}\cup{N}. \\ $$$${An}\:{example}\:{of}\:{f}\left({x}\right)\in{N}\:{is}\: \\ $$$${f}:\:{x}\mid\rightarrow{x}−{cosx}.\:\therefore\:{f}\left({x}\right)={x}−{cosx} \\ $$$${f}\left(−{x}\right)=−{x}−{cosx}\neq{f}\left({x}\right)\:{and} \\ $$$${f}\left(−{x}\right)\neq−{f}\left({x}\right). \\ $$$${Perhaps}\:{one}\:{general}\:{way}\:{to}\:{construct} \\ $$$${some}\:{members}\:{of}\:{N}\:{includes}\:{the}\:{form} \\ $$$${f}\left({x}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{g}_{{i}} \left({x}\right)\:{where}\:{at}\:{least}\:{one} \\ $$$${function}\:{g}_{{i}} \left({x}\right)\:{is}\:{different}\:{in}\:{parity} \\ $$$${from}\:{the}\:{others}\:{for}\:{some}\:{i}\in\left[\mathrm{1},{n}\right]\:{where} \\ $$$${n}\geqslant\mathrm{2}. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Ashis last updated on 08/Jun/16

$${not} \\ $$$${this}\:{depends}\:{on}\:{the}\:{function} \\ $$$${for}\:{example} \\ $$$${let}\:{f}\left({x}\right)={x}^{\mathrm{2}} \\ $$
Commented by FilupSmith last updated on 08/Jun/16

$$\mathrm{I}\:\mathrm{see}. \\ $$$$\mathrm{Lets}\:\mathrm{assume}\:{f}\left({x}\right)\:\mathrm{was}\:\mathrm{a}\:\mathrm{polynomial} \\ $$$$\mathrm{with}\:\mathrm{no}\:\mathrm{constant}\:\mathrm{terms} \\ $$$$\mathrm{i}.\mathrm{e}. \\ $$$${f}\left({x}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} {x}^{{e}_{{i}} } ,\:\:\:\:\forall{i},\:{e}_{{i}} \neq\mathrm{0} \\ $$$$\mathrm{let}\:\mathrm{the}\:\mathrm{greatest}\:\mathrm{exponent}\:\mathrm{be}\:\mathrm{odd}, \\ $$$${that}\:{is}:\:{e}_{{n}} \in\mathbb{O} \\ $$$$\mathrm{is}\:{f}\left(\mathrm{1}\right){f}\left(−\mathrm{1}\right)\leqslant\mathrm{0} \\ $$$$ \\ $$$${e}.{g}.\:{x}^{\mathrm{3}} −{x}^{\mathrm{2}} ,\:\:{x}^{\mathrm{7}} +{x}^{\mathrm{5}} +{x}^{\mathrm{4}} ,\:{etc} \\ $$
Commented by FilupSmith last updated on 09/Jun/16
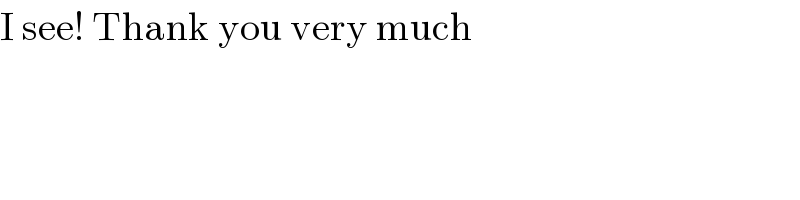
$$\mathrm{I}\:\mathrm{see}!\:\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much} \\ $$
Commented by Rasheed Soomro last updated on 09/Jun/16
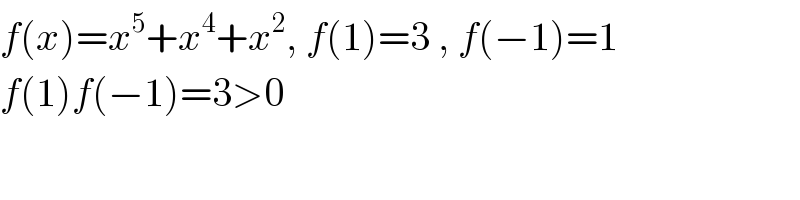
$${f}\left({x}\right)={x}^{\mathrm{5}} +{x}^{\mathrm{4}} +{x}^{\mathrm{2}} ,\:{f}\left(\mathrm{1}\right)=\mathrm{3}\:,\:{f}\left(−\mathrm{1}\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right){f}\left(−\mathrm{1}\right)=\mathrm{3}>\mathrm{0} \\ $$
