Menu Close

f-f-x-f-f-x-f-x-

Tinku Tara 0 Comments
Pin




Question Number 2035 by Rasheed Soomro last updated on 31/Oct/15
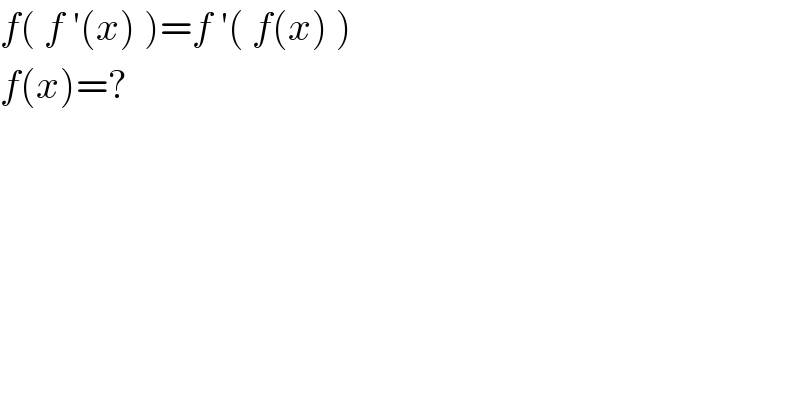
f( f ′(x) )=f ′( f(x) ) f(x)=?
$${f}\left(\:{f}\:'\left({x}\right)\:\right)={f}\:'\left(\:{f}\left({x}\right)\:\right) \\ $$$${f}\left({x}\right)=? \\ $$
Commented by Yozzi last updated on 31/Oct/15
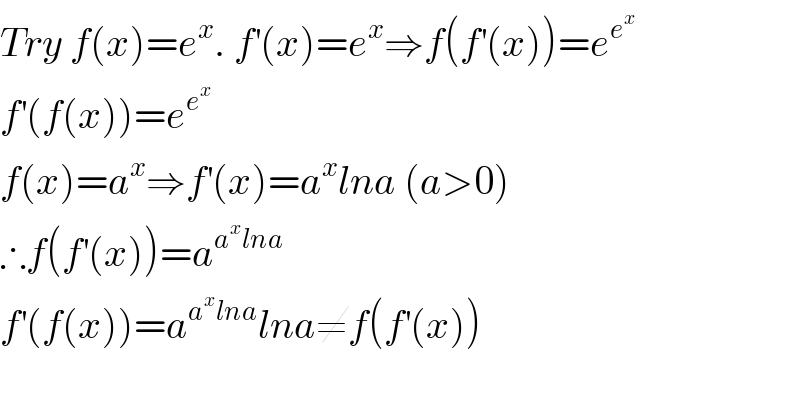
Try f(x)=e^x . f^′ (x)=e^x ⇒f(f^′ (x))=e^e^x f^′ (f(x))=e^e^x f(x)=a^x ⇒f^′ (x)=a^x lna (a>0) ∴f(f^′ (x))=a^(a^x lna) f^′ (f(x))=a^(a^x lna) lna≠f(f^′ (x))
$${Try}\:{f}\left({x}\right)={e}^{{x}} .\:{f}^{'} \left({x}\right)={e}^{{x}} \Rightarrow{f}\left({f}^{'} \left({x}\right)\right)={e}^{{e}^{{x}} } \\ $$$${f}^{'} \left({f}\left({x}\right)\right)={e}^{{e}^{{x}} } \\ $$$${f}\left({x}\right)={a}^{{x}} \Rightarrow{f}^{'} \left({x}\right)={a}^{{x}} {lna}\:\left({a}>\mathrm{0}\right) \\ $$$$\therefore{f}\left({f}^{'} \left({x}\right)\right)={a}^{{a}^{{x}} {lna}} \\ $$$${f}^{'} \left({f}\left({x}\right)\right)={a}^{{a}^{{x}} {lna}} {lna}\neq{f}\left({f}^{'} \left({x}\right)\right) \\ $$$$ \\ $$
Commented by 123456 last updated on 31/Oct/15
f•f^(−1) =f^(−1) •f=I (if f is invertible) f[f′(x)]=f′[f(x)] f′(x)=f^(−1) {f′[f(x)]} f(x)=(f′)^(−1) {f[f′(x)]}
$${f}\bullet{f}^{−\mathrm{1}} ={f}^{−\mathrm{1}} \bullet{f}=\mathrm{I}\:\:\left(\mathrm{if}\:{f}\:\mathrm{is}\:\mathrm{invertible}\right) \\ $$$${f}\left[{f}'\left({x}\right)\right]={f}'\left[{f}\left({x}\right)\right] \\ $$$${f}'\left({x}\right)={f}^{−\mathrm{1}} \left\{{f}'\left[{f}\left({x}\right)\right]\right\} \\ $$$${f}\left({x}\right)=\left({f}'\right)^{−\mathrm{1}} \left\{{f}\left[{f}'\left({x}\right)\right]\right\} \\ $$
Answered by 123456 last updated on 31/Oct/15
f(x)=a^x f′(x)=a^x ln a (a>0) f[f′(x)]=a^(a^x ln a) f′[f(x)]=a^a^x ln a a^(a^x ln a) =a^a^x ln a a^(a^x (ln a−1)) =ln a (a^a^x ≠0) a^x (ln a−1)=log_a ln a (ln a>0⇒a>1) a^x =((log_a ln a)/(ln a−1)) (ln a≠1⇒a≠e) x=log_a (((log_a ln a)/(ln a−1))) −−−−−−−−−− a=e⇒ln a=1⇒log_a ln a=0 f(x)=e^x is a solution
$${f}\left({x}\right)={a}^{{x}} \\ $$$${f}'\left({x}\right)={a}^{{x}} \mathrm{ln}\:{a}\:\:\:\:\:\:\:\:\:\:\left({a}>\mathrm{0}\right) \\ $$$${f}\left[{f}'\left({x}\right)\right]={a}^{{a}^{{x}} \mathrm{ln}\:{a}} \\ $$$${f}'\left[{f}\left({x}\right)\right]={a}^{{a}^{{x}} } \mathrm{ln}\:{a} \\ $$$${a}^{{a}^{{x}} \mathrm{ln}\:{a}} ={a}^{{a}^{{x}} } \mathrm{ln}\:{a}\:\:\:\:\:\: \\ $$$${a}^{{a}^{{x}} \left(\mathrm{ln}\:{a}−\mathrm{1}\right)} =\mathrm{ln}\:{a}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left({a}^{{a}^{{x}} } \neq\mathrm{0}\right) \\ $$$${a}^{{x}} \left(\mathrm{ln}\:{a}−\mathrm{1}\right)=\mathrm{log}_{{a}} \mathrm{ln}\:{a}\:\:\left(\mathrm{ln}\:{a}>\mathrm{0}\Rightarrow{a}>\mathrm{1}\right) \\ $$$${a}^{{x}} =\frac{\mathrm{log}_{{a}} \mathrm{ln}\:{a}}{\mathrm{ln}\:{a}−\mathrm{1}}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{ln}\:{a}\neq\mathrm{1}\Rightarrow{a}\neq{e}\right) \\ $$$${x}=\mathrm{log}_{{a}} \left(\frac{\mathrm{log}_{{a}} \mathrm{ln}\:{a}}{\mathrm{ln}\:{a}−\mathrm{1}}\right) \\ $$$$−−−−−−−−−− \\ $$$${a}={e}\Rightarrow\mathrm{ln}\:{a}=\mathrm{1}\Rightarrow\mathrm{log}_{{a}} \:\mathrm{ln}\:{a}=\mathrm{0} \\ $$$${f}\left({x}\right)={e}^{{x}} \:\:\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution} \\ $$
Answered by prakash jain last updated on 31/Oct/15
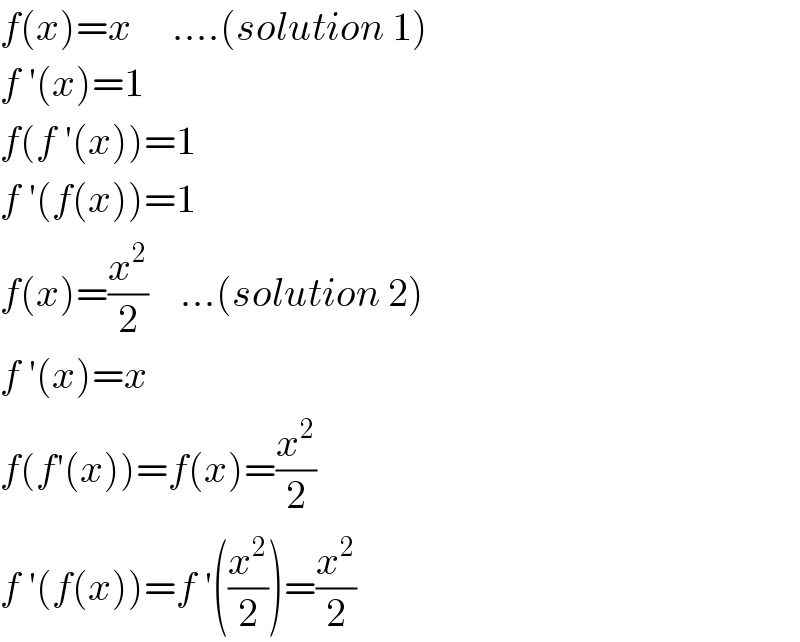
f(x)=x ....(solution 1) f ′(x)=1 f(f ′(x))=1 f ′(f(x))=1 f(x)=(x^2 /2) ...(solution 2) f ′(x)=x f(f′(x))=f(x)=(x^2 /2) f ′(f(x))=f ′((x^2 /2))=(x^2 /2)
$${f}\left({x}\right)={x}\:\:\:\:\:….\left({solution}\:\mathrm{1}\right) \\ $$$${f}\:'\left({x}\right)=\mathrm{1} \\ $$$${f}\left({f}\:'\left({x}\right)\right)=\mathrm{1} \\ $$$${f}\:'\left({f}\left({x}\right)\right)=\mathrm{1} \\ $$$${f}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\:\:\:…\left({solution}\:\mathrm{2}\right) \\ $$$${f}\:'\left({x}\right)={x} \\ $$$${f}\left({f}'\left({x}\right)\right)={f}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${f}\:'\left({f}\left({x}\right)\right)={f}\:'\left(\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by prakash jain last updated on 31/Oct/15
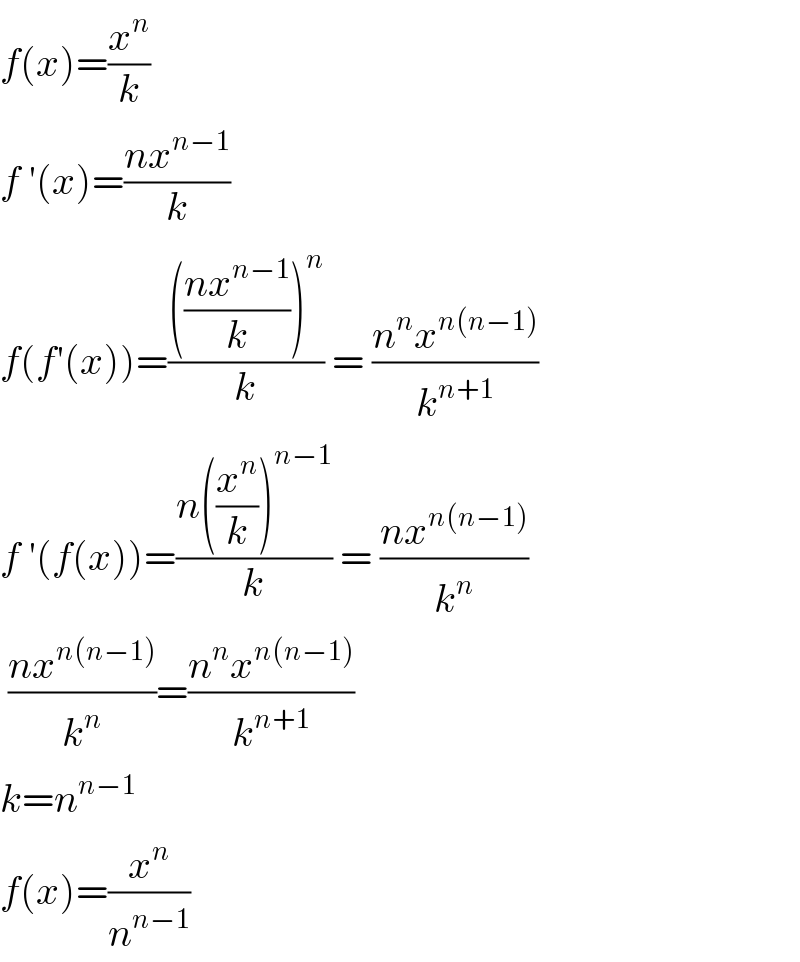
f(x)=(x^n /k) f ′(x)=((nx^(n−1) )/k) f(f′(x))=(((((nx^(n−1) )/k))^n )/k) = ((n^n x^(n(n−1)) )/k^(n+1) ) f ′(f(x))=((n((x^n /k))^(n−1) )/k) = ((nx^(n(n−1)) )/k^n ) ((nx^(n(n−1)) )/k^n )=((n^n x^(n(n−1)) )/k^(n+1) ) k=n^(n−1) f(x)=(x^n /n^(n−1) )
$${f}\left({x}\right)=\frac{{x}^{{n}} }{{k}} \\ $$$${f}\:'\left({x}\right)=\frac{{nx}^{{n}−\mathrm{1}} }{{k}} \\ $$$${f}\left({f}'\left({x}\right)\right)=\frac{\left(\frac{{nx}^{{n}−\mathrm{1}} }{{k}}\right)^{{n}} }{{k}}\:=\:\frac{{n}^{{n}} {x}^{{n}\left({n}−\mathrm{1}\right)} }{{k}^{{n}+\mathrm{1}} } \\ $$$${f}\:'\left({f}\left({x}\right)\right)=\frac{{n}\left(\frac{{x}^{{n}} }{{k}}\right)^{{n}−\mathrm{1}} }{{k}}\:=\:\frac{{nx}^{{n}\left({n}−\mathrm{1}\right)} }{{k}^{{n}} } \\ $$$$\:\frac{{nx}^{{n}\left({n}−\mathrm{1}\right)} }{{k}^{{n}} }=\frac{{n}^{{n}} {x}^{{n}\left({n}−\mathrm{1}\right)} }{{k}^{{n}+\mathrm{1}} } \\ $$$${k}={n}^{{n}−\mathrm{1}} \\ $$$${f}\left({x}\right)=\frac{{x}^{{n}} }{{n}^{{n}−\mathrm{1}} }\:\:\: \\ $$
Commented by Rasheed Soomro last updated on 01/Nov/15
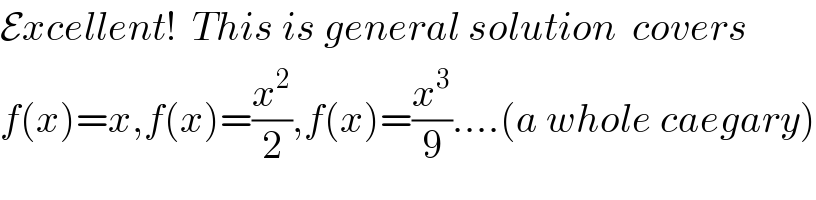
Excellent! This is general solution covers f(x)=x,f(x)=(x^2 /2),f(x)=(x^3 /9)....(a whole caegary)
$$\mathcal{E}{xcellent}!\:\:{This}\:{is}\:{general}\:{solution}\:\:{covers} \\ $$$${f}\left({x}\right)={x},{f}\left({x}\right)=\frac{{x}^{\mathrm{2}} }{\mathrm{2}},{f}\left({x}\right)=\frac{{x}^{\mathrm{3}} }{\mathrm{9}}….\left({a}\:{whole}\:{caegary}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *