Question Number 2253 by 123456 last updated on 11/Nov/15
![f_n :[0,1]→[0,1],g:[0,1]→[0,1] f_(n+1) (x)=g[f_n (x)]+f_n [g(x)] f_0 (x)=x f_4 (x)=? g(x)=x^2 ,f_2 (2)=??](https://www.tinkutara.com/question/Q2253.png)
$${f}_{{n}} :\left[\mathrm{0},\mathrm{1}\right]\rightarrow\left[\mathrm{0},\mathrm{1}\right],{g}:\left[\mathrm{0},\mathrm{1}\right]\rightarrow\left[\mathrm{0},\mathrm{1}\right] \\ $$$${f}_{{n}+\mathrm{1}} \left({x}\right)={g}\left[{f}_{{n}} \left({x}\right)\right]+{f}_{{n}} \left[{g}\left({x}\right)\right] \\ $$$${f}_{\mathrm{0}} \left({x}\right)={x} \\ $$$${f}_{\mathrm{4}} \left({x}\right)=? \\ $$$${g}\left({x}\right)={x}^{\mathrm{2}} ,{f}_{\mathrm{2}} \left(\mathrm{2}\right)=?? \\ $$
Commented by RasheedAhmad last updated on 12/Nov/15
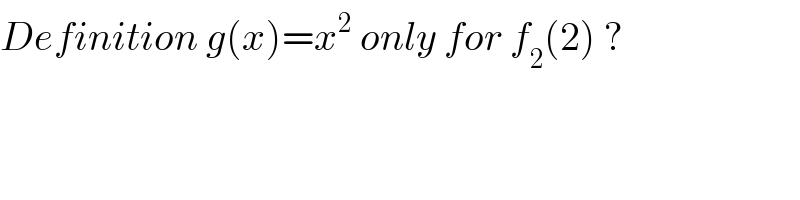
$${Definition}\:{g}\left({x}\right)={x}^{\mathrm{2}} \:{only}\:{for}\:{f}_{\mathrm{2}} \left(\mathrm{2}\right)\:? \\ $$
Answered by prakash jain last updated on 12/Nov/15
![f_1 (x)=g[f_0 (x)]+f_0 [g(x)]=g(x)+g(x)=2g(x) f_1 (x)=2x^2 f_2 (x)=g(2x^2 )+f_1 (x^2 )=4x^4 +2x^4 =6x^4 f_3 (x)=(6x^4 )^2 +6x^8 =42x^8 f_4 (x)=(42x^8 )^2 +42(x^2 )^8 =42×43x^(16)](https://www.tinkutara.com/question/Q2262.png)
$${f}_{\mathrm{1}} \left({x}\right)={g}\left[{f}_{\mathrm{0}} \left({x}\right)\right]+{f}_{\mathrm{0}} \left[{g}\left({x}\right)\right]={g}\left({x}\right)+{g}\left({x}\right)=\mathrm{2}{g}\left({x}\right) \\ $$$${f}_{\mathrm{1}} \left({x}\right)=\mathrm{2}{x}^{\mathrm{2}} \\ $$$${f}_{\mathrm{2}} \left({x}\right)={g}\left(\mathrm{2}{x}^{\mathrm{2}} \right)+{f}_{\mathrm{1}} \left({x}^{\mathrm{2}} \right)=\mathrm{4}{x}^{\mathrm{4}} +\mathrm{2}{x}^{\mathrm{4}} =\mathrm{6}{x}^{\mathrm{4}} \\ $$$${f}_{\mathrm{3}} \left({x}\right)=\left(\mathrm{6}{x}^{\mathrm{4}} \right)^{\mathrm{2}} +\mathrm{6}{x}^{\mathrm{8}} =\mathrm{42}{x}^{\mathrm{8}} \\ $$$${f}_{\mathrm{4}} \left({x}\right)=\left(\mathrm{42}{x}^{\mathrm{8}} \right)^{\mathrm{2}} +\mathrm{42}\left({x}^{\mathrm{2}} \right)^{\mathrm{8}} =\mathrm{42}×\mathrm{43}{x}^{\mathrm{16}} \\ $$
