Question Number 5585 by 123456 last updated on 21/May/16
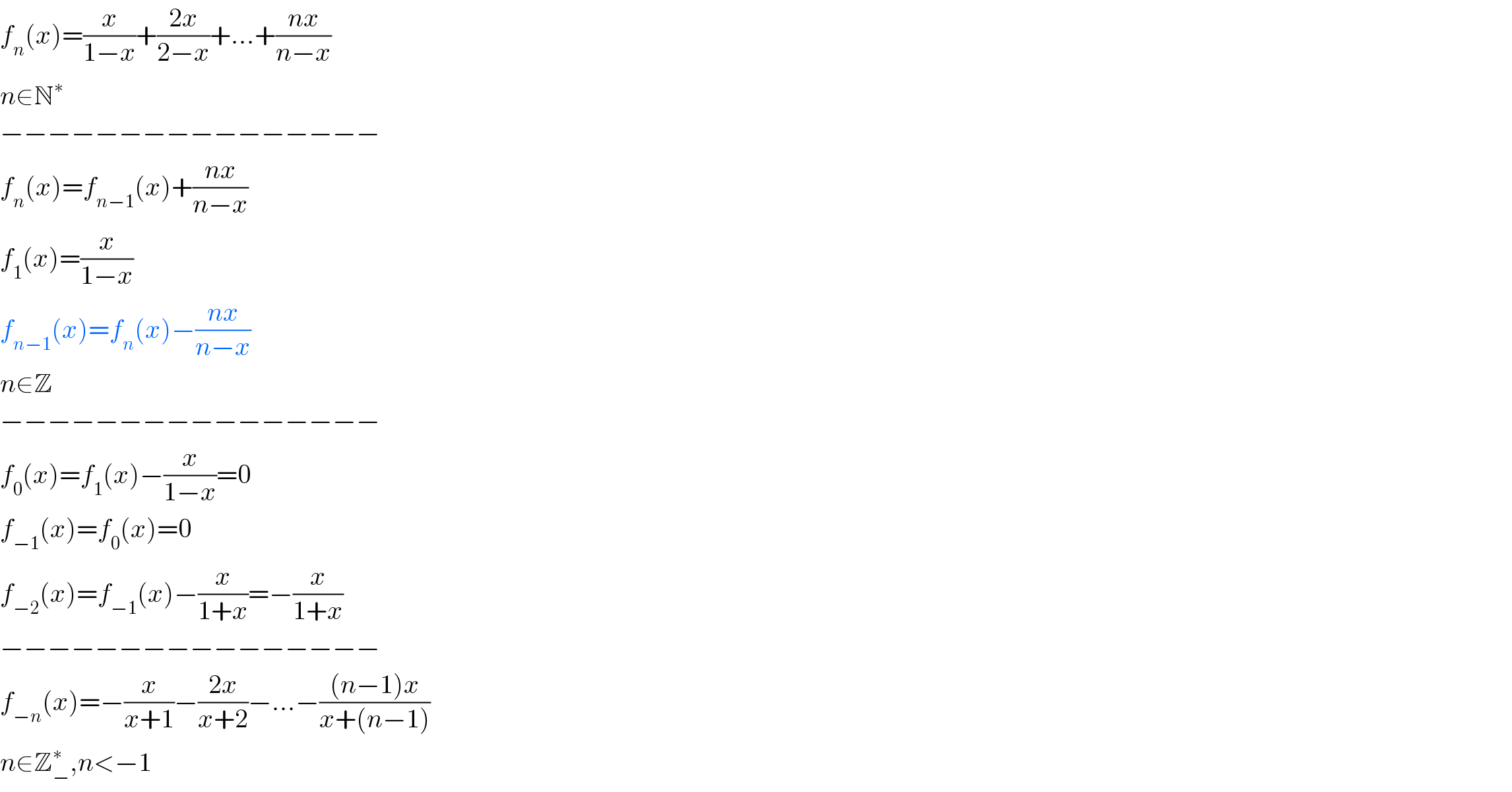
$${f}_{{n}} \left({x}\right)=\frac{{x}}{\mathrm{1}−{x}}+\frac{\mathrm{2}{x}}{\mathrm{2}−{x}}+…+\frac{{nx}}{{n}−{x}} \\ $$$${n}\in\mathbb{N}^{\ast} \\ $$$$−−−−−−−−−−−−−−−− \\ $$$${f}_{{n}} \left({x}\right)={f}_{{n}−\mathrm{1}} \left({x}\right)+\frac{{nx}}{{n}−{x}} \\ $$$${f}_{\mathrm{1}} \left({x}\right)=\frac{{x}}{\mathrm{1}−{x}} \\ $$$${f}_{{n}−\mathrm{1}} \left({x}\right)={f}_{{n}} \left({x}\right)−\frac{{nx}}{{n}−{x}} \\ $$$${n}\in\mathbb{Z} \\ $$$$−−−−−−−−−−−−−−−− \\ $$$${f}_{\mathrm{0}} \left({x}\right)={f}_{\mathrm{1}} \left({x}\right)−\frac{{x}}{\mathrm{1}−{x}}=\mathrm{0} \\ $$$${f}_{−\mathrm{1}} \left({x}\right)={f}_{\mathrm{0}} \left({x}\right)=\mathrm{0} \\ $$$${f}_{−\mathrm{2}} \left({x}\right)={f}_{−\mathrm{1}} \left({x}\right)−\frac{{x}}{\mathrm{1}+{x}}=−\frac{{x}}{\mathrm{1}+{x}} \\ $$$$−−−−−−−−−−−−−−−− \\ $$$${f}_{−{n}} \left({x}\right)=−\frac{{x}}{{x}+\mathrm{1}}−\frac{\mathrm{2}{x}}{{x}+\mathrm{2}}−…−\frac{\left({n}−\mathrm{1}\right){x}}{{x}+\left({n}−\mathrm{1}\right)} \\ $$$${n}\in\mathbb{Z}_{−} ^{\ast} ,{n}<−\mathrm{1} \\ $$
Commented by Rasheed Soomro last updated on 21/May/16
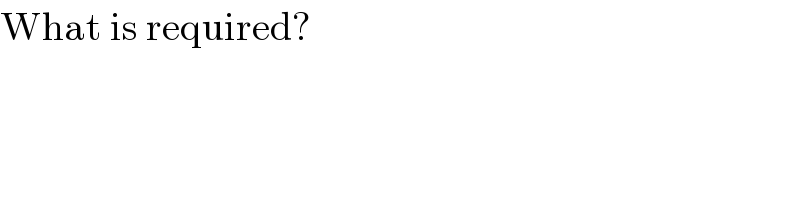
$$\mathrm{What}\:\mathrm{is}\:\mathrm{required}? \\ $$
Commented by 123456 last updated on 21/May/16

$$\frac{{df}_{{n}} }{{dx}} \\ $$
Commented by FilupSmith last updated on 22/May/16

$${f}_{{n}} \left({x}\right)=\frac{{x}}{\mathrm{1}−{x}}+\frac{\mathrm{2}{x}}{\mathrm{2}−{x}}+…+\frac{{nx}}{{n}−{x}} \\ $$$${f}_{{n}} \left({x}\right)=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{ix}}{{i}−{x}} \\ $$$$\frac{{df}_{{n}} }{{dx}}=\frac{{d}}{{dx}}\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{ix}}{{i}−{x}} \\ $$$$\frac{{df}_{{n}} }{{dx}}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{i}\left({i}−{x}\right)+{ix}}{\left({i}−{x}\right)^{\mathrm{2}} }\:\:\:\:\:{quotant}\:{rule} \\ $$$$\frac{{df}_{{n}} }{{dx}}=\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{i}^{\mathrm{2}} }{\left({i}−{x}\right)^{\mathrm{2}} } \\ $$$$???? \\ $$
