Question Number 2524 by 123456 last updated on 21/Nov/15
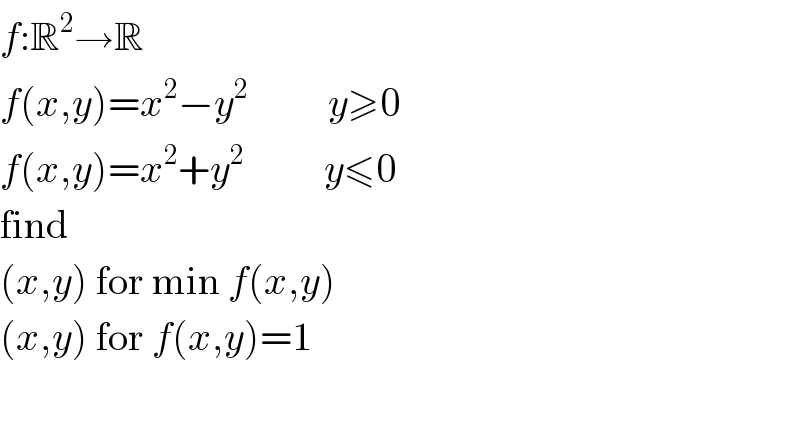
$${f}:\mathbb{R}^{\mathrm{2}} \rightarrow\mathbb{R} \\ $$$${f}\left({x},{y}\right)={x}^{\mathrm{2}} −{y}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:{y}\geqslant\mathrm{0} \\ $$$${f}\left({x},{y}\right)={x}^{\mathrm{2}} +{y}^{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:{y}\leqslant\mathrm{0} \\ $$$$\mathrm{find} \\ $$$$\left({x},{y}\right)\:\mathrm{for}\:\mathrm{min}\:{f}\left({x},{y}\right) \\ $$$$\left({x},{y}\right)\:\mathrm{for}\:{f}\left({x},{y}\right)=\mathrm{1} \\ $$$$ \\ $$
Answered by prakash jain last updated on 22/Nov/15
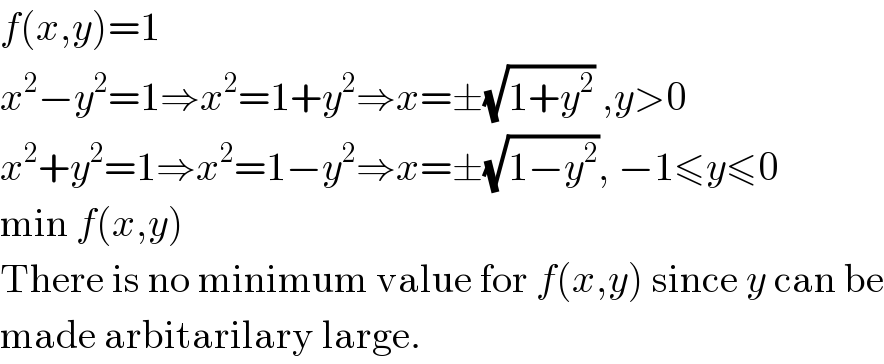
$${f}\left({x},{y}\right)=\mathrm{1} \\ $$$${x}^{\mathrm{2}} −{y}^{\mathrm{2}} =\mathrm{1}\Rightarrow{x}^{\mathrm{2}} =\mathrm{1}+{y}^{\mathrm{2}} \Rightarrow{x}=\pm\sqrt{\mathrm{1}+{y}^{\mathrm{2}} }\:,{y}>\mathrm{0} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{1}\Rightarrow{x}^{\mathrm{2}} =\mathrm{1}−{y}^{\mathrm{2}} \Rightarrow{x}=\pm\sqrt{\mathrm{1}−{y}^{\mathrm{2}} },\:−\mathrm{1}\leqslant{y}\leqslant\mathrm{0} \\ $$$$\mathrm{min}\:{f}\left({x},{y}\right) \\ $$$$\mathrm{There}\:\mathrm{is}\:\mathrm{no}\:\mathrm{minimum}\:\mathrm{value}\:\mathrm{for}\:{f}\left({x},{y}\right)\:\mathrm{since}\:{y}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{made}\:\mathrm{arbitarilary}\:\mathrm{large}. \\ $$
