Question Number 805 by 123456 last updated on 17/Mar/15
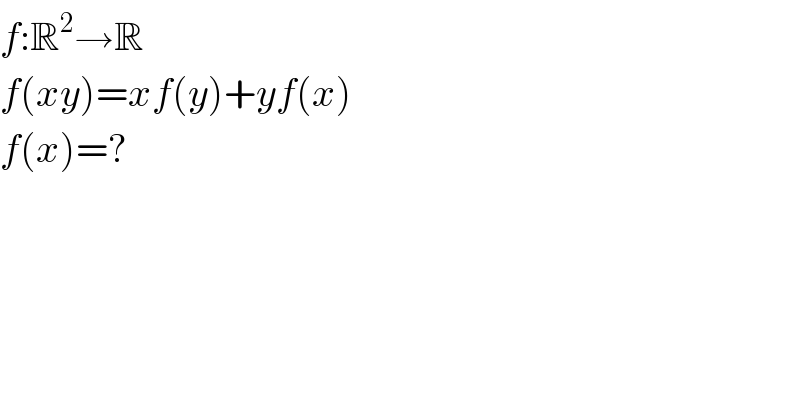
$${f}:\mathbb{R}^{\mathrm{2}} \rightarrow\mathbb{R} \\ $$$${f}\left({xy}\right)={xf}\left({y}\right)+{yf}\left({x}\right) \\ $$$${f}\left({x}\right)=? \\ $$
Answered by prakash jain last updated on 17/Mar/15
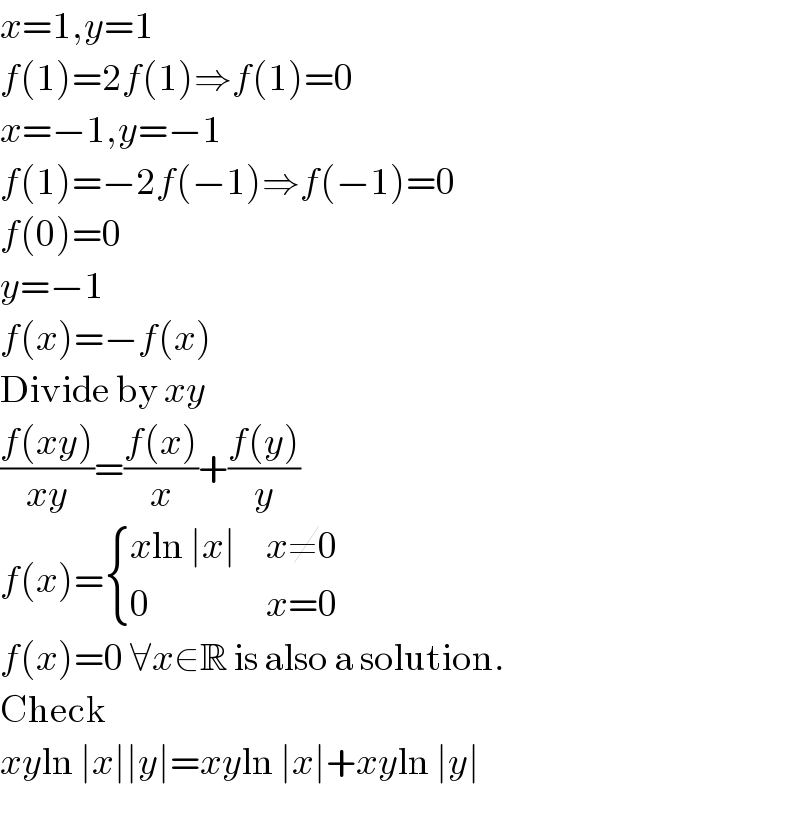
$${x}=\mathrm{1},{y}=\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{2}{f}\left(\mathrm{1}\right)\Rightarrow{f}\left(\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=−\mathrm{1},{y}=−\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=−\mathrm{2}{f}\left(−\mathrm{1}\right)\Rightarrow{f}\left(−\mathrm{1}\right)=\mathrm{0} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${y}=−\mathrm{1} \\ $$$${f}\left({x}\right)=−{f}\left({x}\right) \\ $$$$\mathrm{Divide}\:\mathrm{by}\:{xy} \\ $$$$\frac{{f}\left({xy}\right)}{{xy}}=\frac{{f}\left({x}\right)}{{x}}+\frac{{f}\left({y}\right)}{{y}} \\ $$$${f}\left({x}\right)=\begin{cases}{{x}\mathrm{ln}\:\mid{x}\mid}&{{x}\neq\mathrm{0}}\\{\mathrm{0}}&{{x}=\mathrm{0}}\end{cases} \\ $$$${f}\left({x}\right)=\mathrm{0}\:\forall{x}\in\mathbb{R}\:\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{solution}. \\ $$$$\mathrm{Check} \\ $$$${xy}\mathrm{ln}\:\mid{x}\mid\mid{y}\mid={xy}\mathrm{ln}\:\mid{x}\mid+{xy}\mathrm{ln}\:\mid{y}\mid \\ $$
Commented by prakash jain last updated on 17/Mar/15
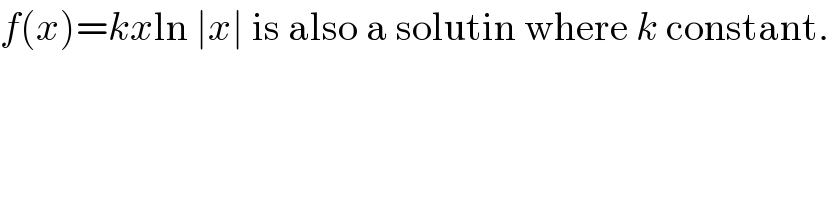
$${f}\left({x}\right)={kx}\mathrm{ln}\:\mid{x}\mid\:\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{solutin}\:\mathrm{where}\:{k}\:\mathrm{constant}. \\ $$
Answered by prakash jain last updated on 17/Mar/15
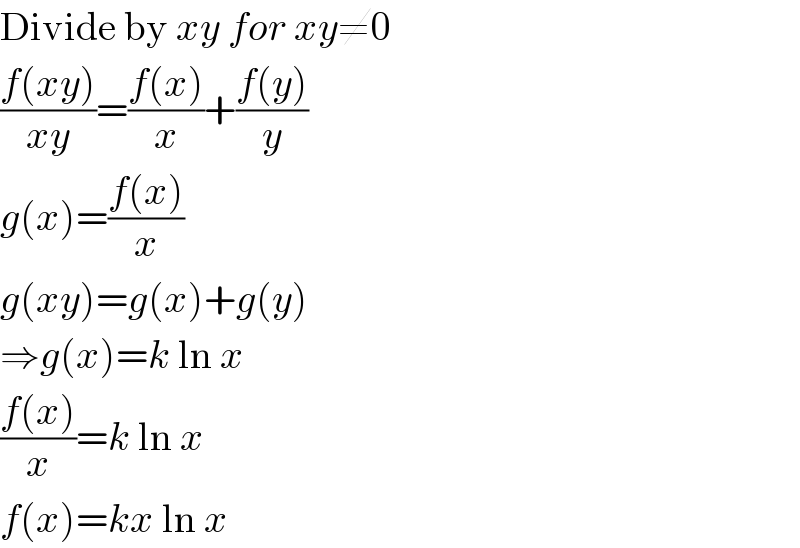
$$\mathrm{Divide}\:\mathrm{by}\:{xy}\:{for}\:{xy}\neq\mathrm{0} \\ $$$$\frac{{f}\left({xy}\right)}{{xy}}=\frac{{f}\left({x}\right)}{{x}}+\frac{{f}\left({y}\right)}{{y}} \\ $$$${g}\left({x}\right)=\frac{{f}\left({x}\right)}{{x}} \\ $$$${g}\left({xy}\right)={g}\left({x}\right)+{g}\left({y}\right) \\ $$$$\Rightarrow{g}\left({x}\right)={k}\:\mathrm{ln}\:{x} \\ $$$$\frac{{f}\left({x}\right)}{{x}}={k}\:\mathrm{ln}\:{x} \\ $$$${f}\left({x}\right)={kx}\:\mathrm{ln}\:{x} \\ $$
