Menu Close

f-R-R-f-x-f-y-f-f-y-xf-y-f-x-1-f-x-

Tinku Tara 0 Comments
Pin




Question Number 3653 by prakash jain last updated on 17/Dec/15
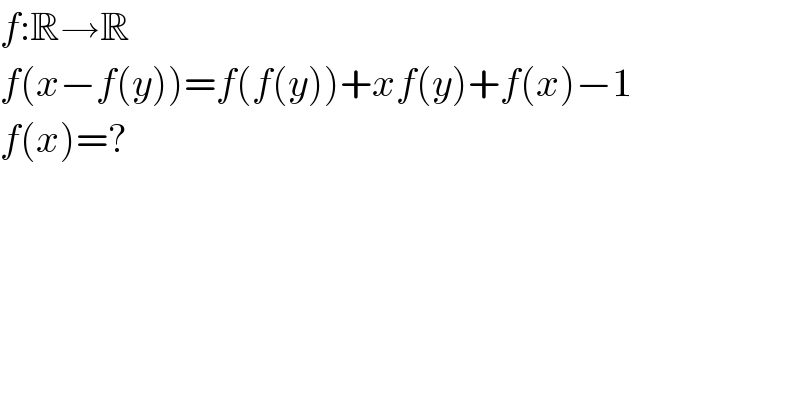
f:R→R f(x−f(y))=f(f(y))+xf(y)+f(x)−1 f(x)=?
$${f}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${f}\left({x}−{f}\left({y}\right)\right)={f}\left({f}\left({y}\right)\right)+{xf}\left({y}\right)+{f}\left({x}\right)−\mathrm{1} \\ $$$${f}\left({x}\right)=? \\ $$
Commented by Rasheed Soomro last updated on 18/Dec/15
f(x−f(y))=f(f(y))+xf(y)+f(x)−1................(i) −−−−−− x=0 in (i) f(0−f(y))=f(f(y))+0f(y)+f(0)−1 f( −f(y) )=f( f(y) )+f(0)−1 −−−−−−− y=0 in (i) f(x−f(0))=f(f(0))+xf(0)+f(x)−1 Let y=x f(x−f(x))=f(f(x))+xf(x)+f(x)−1 f(x−f(x))=f(f(x))+(x+1)f(x)−1 f(x−f(x))−f(f(x))+1=(x+1)f(x) x↔y in (i) f(y−f(x))=f(f(x))+yf(x)+f(y)−1................(ii)
$${f}\left({x}−{f}\left({y}\right)\right)={f}\left({f}\left({y}\right)\right)+{xf}\left({y}\right)+{f}\left({x}\right)−\mathrm{1}…………….\left({i}\right) \\ $$$$−−−−−− \\ $$$${x}=\mathrm{0}\:{in}\:\left({i}\right) \\ $$$${f}\left(\mathrm{0}−{f}\left({y}\right)\right)={f}\left({f}\left({y}\right)\right)+\mathrm{0}{f}\left({y}\right)+{f}\left(\mathrm{0}\right)−\mathrm{1} \\ $$$${f}\left(\:−{f}\left({y}\right)\:\right)={f}\left(\:{f}\left({y}\right)\:\right)+{f}\left(\mathrm{0}\right)−\mathrm{1} \\ $$$$−−−−−−− \\ $$$${y}=\mathrm{0}\:{in}\:\left({i}\right) \\ $$$${f}\left({x}−{f}\left(\mathrm{0}\right)\right)={f}\left({f}\left(\mathrm{0}\right)\right)+{xf}\left(\mathrm{0}\right)+{f}\left({x}\right)−\mathrm{1} \\ $$$${Let}\:{y}={x} \\ $$$${f}\left({x}−{f}\left({x}\right)\right)={f}\left({f}\left({x}\right)\right)+{xf}\left({x}\right)+{f}\left({x}\right)−\mathrm{1} \\ $$$${f}\left({x}−{f}\left({x}\right)\right)={f}\left({f}\left({x}\right)\right)+\left({x}+\mathrm{1}\right){f}\left({x}\right)−\mathrm{1} \\ $$$${f}\left({x}−{f}\left({x}\right)\right)−{f}\left({f}\left({x}\right)\right)+\mathrm{1}=\left({x}+\mathrm{1}\right){f}\left({x}\right) \\ $$$${x}\leftrightarrow{y}\:\:{in}\:\:\left({i}\right) \\ $$$${f}\left({y}−{f}\left({x}\right)\right)={f}\left({f}\left({x}\right)\right)+{yf}\left({x}\right)+{f}\left({y}\right)−\mathrm{1}…………….\left({ii}\right) \\ $$
Commented by prakash jain last updated on 18/Dec/15
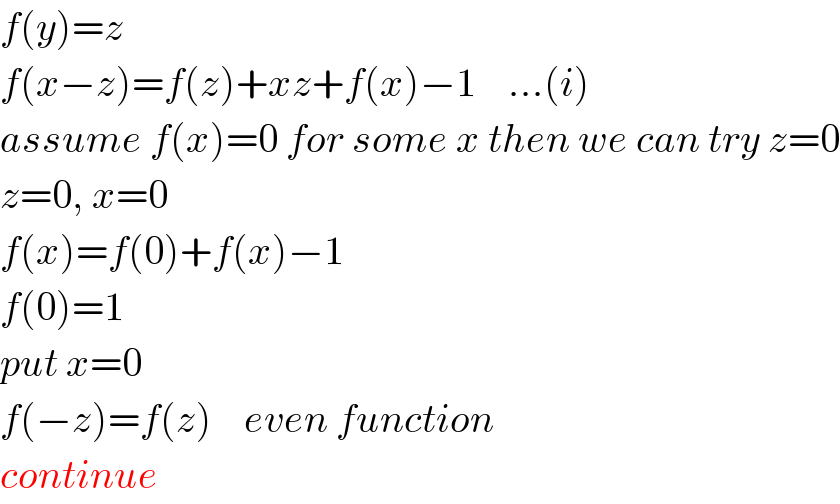
f(y)=z f(x−z)=f(z)+xz+f(x)−1 ...(i) assume f(x)=0 for some x then we can try z=0 z=0, x=0 f(x)=f(0)+f(x)−1 f(0)=1 put x=0 f(−z)=f(z) even function continue
$${f}\left({y}\right)={z} \\ $$$${f}\left({x}−{z}\right)={f}\left({z}\right)+{xz}+{f}\left({x}\right)−\mathrm{1}\:\:\:\:…\left({i}\right) \\ $$$${assume}\:{f}\left({x}\right)=\mathrm{0}\:{for}\:{some}\:{x}\:{then}\:{we}\:{can}\:{try}\:{z}=\mathrm{0} \\ $$$${z}=\mathrm{0},\:{x}=\mathrm{0} \\ $$$${f}\left({x}\right)={f}\left(\mathrm{0}\right)+{f}\left({x}\right)−\mathrm{1} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{1} \\ $$$${put}\:{x}=\mathrm{0} \\ $$$${f}\left(−{z}\right)={f}\left({z}\right)\:\:\:\:{even}\:{function} \\ $$$${continue} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *