Question Number 818 by 123456 last updated on 17/Mar/15
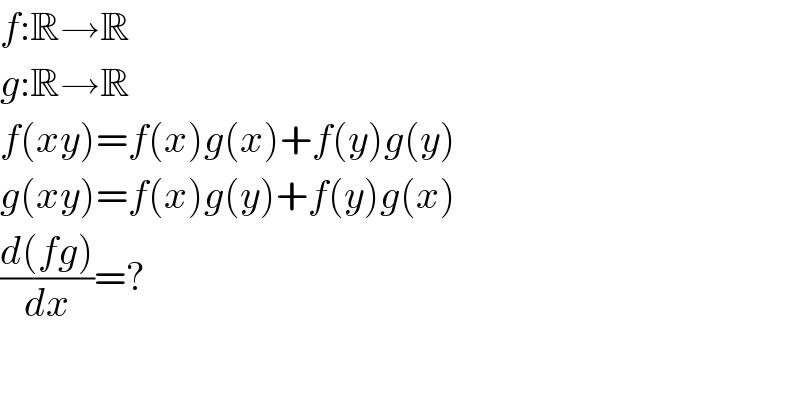
$${f}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${g}:\mathbb{R}\rightarrow\mathbb{R} \\ $$$${f}\left({xy}\right)={f}\left({x}\right){g}\left({x}\right)+{f}\left({y}\right){g}\left({y}\right) \\ $$$${g}\left({xy}\right)={f}\left({x}\right){g}\left({y}\right)+{f}\left({y}\right){g}\left({x}\right) \\ $$$$\frac{{d}\left({fg}\right)}{{dx}}=? \\ $$
Commented by prakash jain last updated on 17/Mar/15
![x=1, y=1 f(1)=2f(1)g(1) g(1)=2f(1)g(1) f(1)=g(1) f(1)=2[f(1)]^2 f(1)=0 ∨f(1)=(1/2) If f(1)=0, g(1)=f(1)=0, f(x)=g(x)=0 If f(1)=(1/2), g(1)=f(1)=(1/2) g(x)=(1/2)[f(x)+g(x)]⇒f(x)=g(x) f(x)=[f(x)]^2 +(1/4) f(x)=g(x)=(1/2)](https://www.tinkutara.com/question/Q819.png)
$${x}=\mathrm{1},\:{y}=\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{2}{f}\left(\mathrm{1}\right){g}\left(\mathrm{1}\right) \\ $$$${g}\left(\mathrm{1}\right)=\mathrm{2}{f}\left(\mathrm{1}\right){g}\left(\mathrm{1}\right) \\ $$$${f}\left(\mathrm{1}\right)={g}\left(\mathrm{1}\right) \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{2}\left[{f}\left(\mathrm{1}\right)\right]^{\mathrm{2}} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0}\:\vee{f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{If}\:{f}\left(\mathrm{1}\right)=\mathrm{0},\:\:{g}\left(\mathrm{1}\right)={f}\left(\mathrm{1}\right)=\mathrm{0},\:{f}\left({x}\right)={g}\left({x}\right)=\mathrm{0} \\ $$$$\mathrm{If}\:{f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}},\:{g}\left(\mathrm{1}\right)={f}\left(\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${g}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left[{f}\left({x}\right)+{g}\left({x}\right)\right]\Rightarrow{f}\left({x}\right)={g}\left({x}\right) \\ $$$${f}\left({x}\right)=\left[{f}\left({x}\right)\right]^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${f}\left({x}\right)={g}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Answered by prakash jain last updated on 17/Mar/15
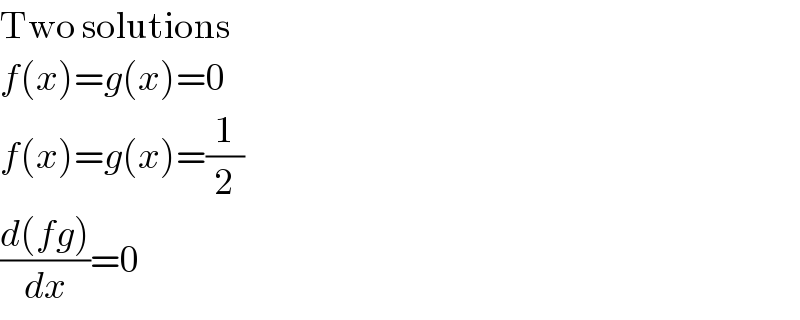
$$\mathrm{Two}\:\mathrm{solutions} \\ $$$${f}\left({x}\right)={g}\left({x}\right)=\mathrm{0} \\ $$$${f}\left({x}\right)={g}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{d}\left({fg}\right)}{{dx}}=\mathrm{0} \\ $$
