Question Number 131807 by Fikret last updated on 08/Feb/21
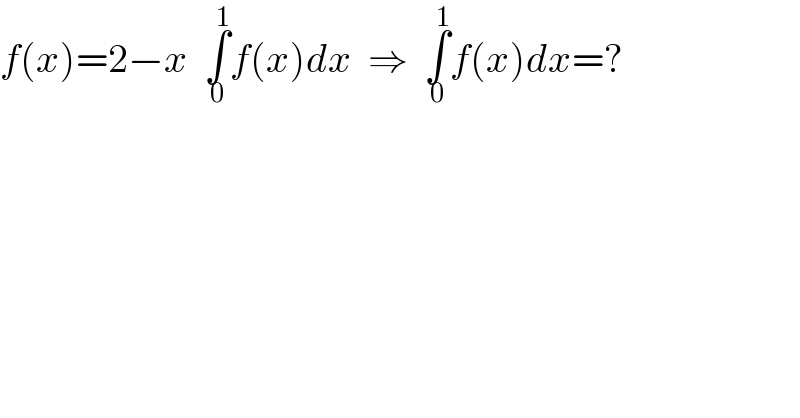
$${f}\left({x}\right)=\mathrm{2}−{x}\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx}\:\:\Rightarrow\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx}=? \\ $$$$ \\ $$$$ \\ $$
Commented by Fikret last updated on 08/Feb/21
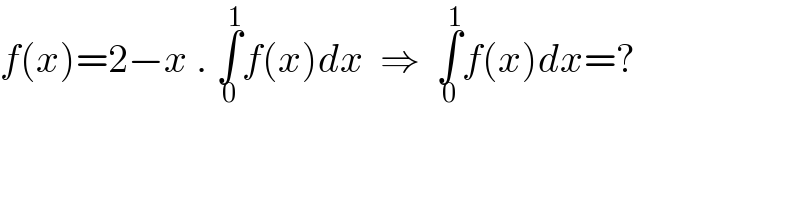
$${f}\left({x}\right)=\mathrm{2}−{x}\:.\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx}\:\:\Rightarrow\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{f}\left({x}\right){dx}=? \\ $$$$ \\ $$$$ \\ $$
Answered by mr W last updated on 08/Feb/21
![say ∫_0 ^1 f(x)dx=c f(x)=2−cx ∫_0 ^1 f(x)dx=[2x−((cx^2 )/2)]_0 ^1 =2−(c/2)=c ⇒c=(4/3)=∫_0 ^1 f(x)dx](https://www.tinkutara.com/question/Q131811.png)
$${say}\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}={c} \\ $$$${f}\left({x}\right)=\mathrm{2}−{cx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx}=\left[\mathrm{2}{x}−\frac{{cx}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\mathrm{2}−\frac{{c}}{\mathrm{2}}={c} \\ $$$$\Rightarrow{c}=\frac{\mathrm{4}}{\mathrm{3}}=\int_{\mathrm{0}} ^{\mathrm{1}} {f}\left({x}\right){dx} \\ $$
