Question Number 66149 by Rio Michael last updated on 09/Aug/19
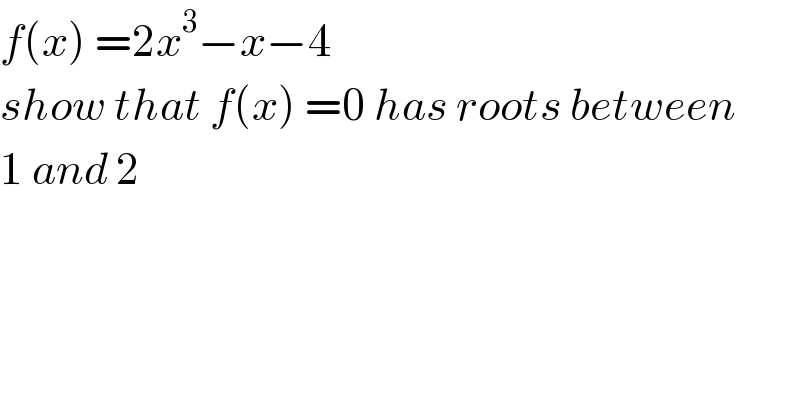
$${f}\left({x}\right)\:=\mathrm{2}{x}^{\mathrm{3}} −{x}−\mathrm{4}\: \\ $$$${show}\:{that}\:{f}\left({x}\right)\:=\mathrm{0}\:{has}\:{roots}\:{between} \\ $$$$\mathrm{1}\:{and}\:\mathrm{2} \\ $$
Answered by MJS last updated on 09/Aug/19

$${f}\left(\mathrm{1}\right)=−\mathrm{3}<\mathrm{0} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{10}>\mathrm{0} \\ $$$$\mathrm{and}\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{continuous}\:\mathrm{for}\:{x}\in\mathbb{R} \\ $$$$\Rightarrow\:\mathrm{there}\:\mathrm{nust}\:\mathrm{be}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one}\:\mathrm{zero}\:\mathrm{between} \\ $$$${x}=\mathrm{1}\:\mathrm{and}\:{x}=\mathrm{2} \\ $$
Answered by mr W last updated on 09/Aug/19
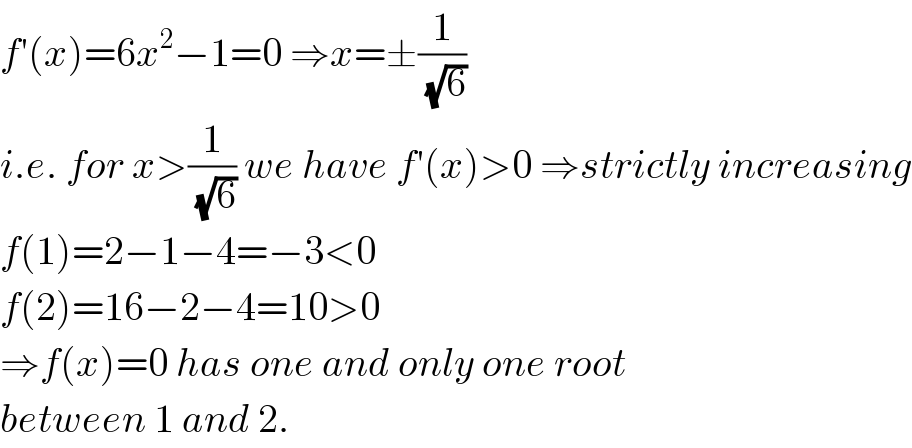
$${f}'\left({x}\right)=\mathrm{6}{x}^{\mathrm{2}} −\mathrm{1}=\mathrm{0}\:\Rightarrow{x}=\pm\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}} \\ $$$${i}.{e}.\:{for}\:{x}>\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}}\:{we}\:{have}\:{f}'\left({x}\right)>\mathrm{0}\:\Rightarrow{strictly}\:{increasing} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{2}−\mathrm{1}−\mathrm{4}=−\mathrm{3}<\mathrm{0} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{16}−\mathrm{2}−\mathrm{4}=\mathrm{10}>\mathrm{0} \\ $$$$\Rightarrow{f}\left({x}\right)=\mathrm{0}\:{has}\:{one}\:{and}\:{only}\:{one}\:{root} \\ $$$${between}\:\mathrm{1}\:{and}\:\mathrm{2}. \\ $$
