Question Number 11899 by ahmet last updated on 04/Apr/17
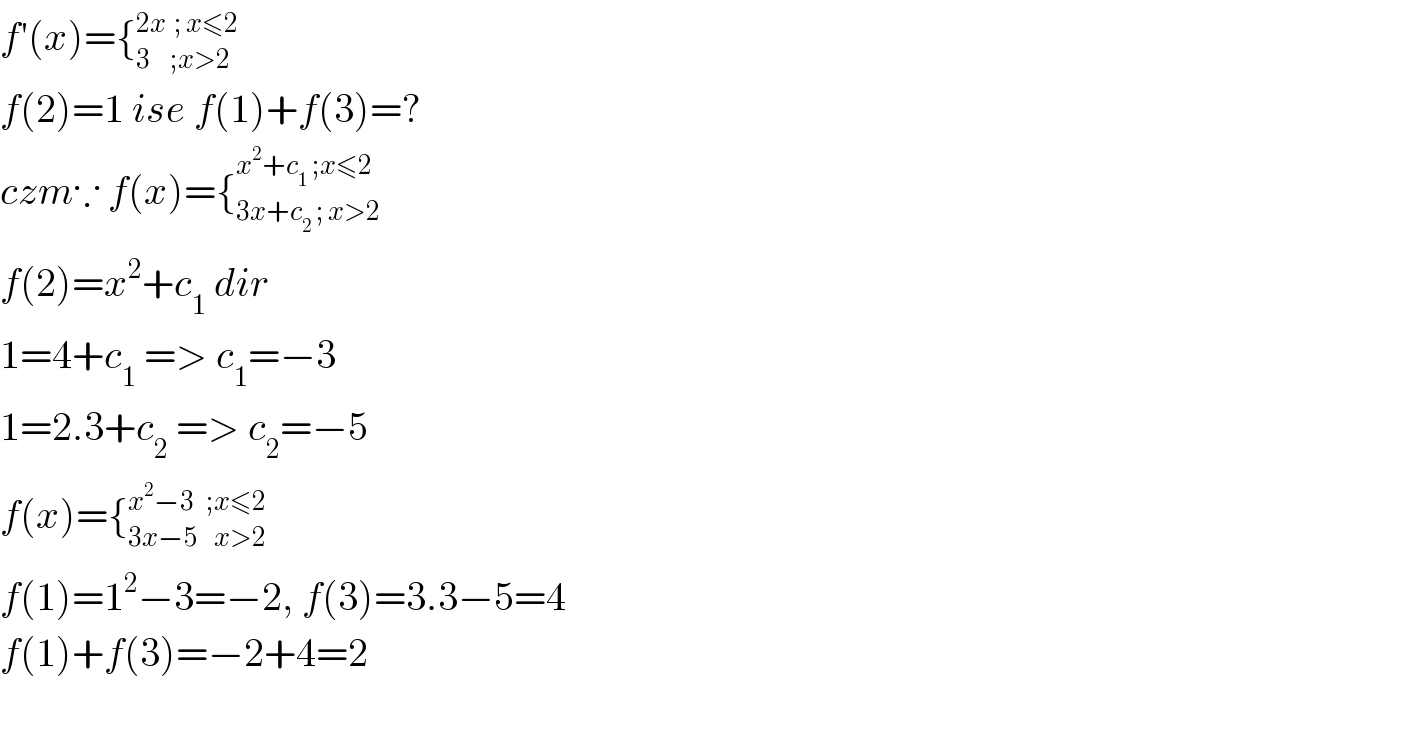
$${f}'\left({x}\right)=\left\{_{\mathrm{3}\:\:\:\:\:;{x}>\mathrm{2}} ^{\mathrm{2}{x}\:\:;\:{x}\leqslant\mathrm{2}} \right. \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{1}\:{ise}\:{f}\left(\mathrm{1}\right)+{f}\left(\mathrm{3}\right)=? \\ $$$${czm}\because\:{f}\left({x}\right)=\left\{_{\mathrm{3}{x}+{c}_{\mathrm{2}} \:;\:{x}>\mathrm{2}} ^{{x}^{\mathrm{2}} +{c}_{\mathrm{1}} \:;{x}\leqslant\mathrm{2}} \right. \\ $$$${f}\left(\mathrm{2}\right)={x}^{\mathrm{2}} +{c}_{\mathrm{1}} \:{dir} \\ $$$$\mathrm{1}=\mathrm{4}+{c}_{\mathrm{1}} \:=>\:{c}_{\mathrm{1}} =−\mathrm{3} \\ $$$$\mathrm{1}=\mathrm{2}.\mathrm{3}+{c}_{\mathrm{2}} \:=>\:{c}_{\mathrm{2}} =−\mathrm{5} \\ $$$${f}\left({x}\right)=\left\{_{\mathrm{3}{x}−\mathrm{5}\:\:\:\:{x}>\mathrm{2}} ^{{x}^{\mathrm{2}} −\mathrm{3}\:\:\:;{x}\leqslant\mathrm{2}} \right. \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{1}^{\mathrm{2}} −\mathrm{3}=−\mathrm{2},\:{f}\left(\mathrm{3}\right)=\mathrm{3}.\mathrm{3}−\mathrm{5}=\mathrm{4} \\ $$$${f}\left(\mathrm{1}\right)+{f}\left(\mathrm{3}\right)=−\mathrm{2}+\mathrm{4}=\mathrm{2} \\ $$$$ \\ $$
