Question Number 131206 by Study last updated on 02/Feb/21

$${f}\left({x}\right)=\infty \\ $$$$\frac{{d}}{{dx}}{f}\left({x}\right)=? \\ $$
Commented by mr W last updated on 02/Feb/21
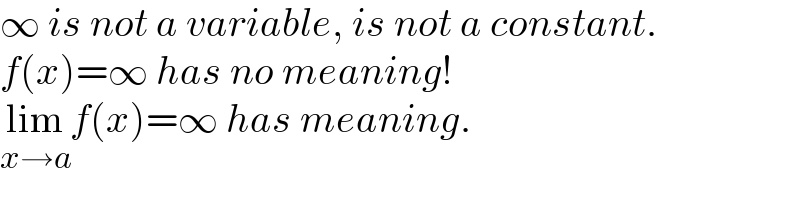
$$\infty\:{is}\:{not}\:{a}\:{variable},\:{is}\:{not}\:{a}\:{constant}. \\ $$$${f}\left({x}\right)=\infty\:{has}\:{no}\:{meaning}! \\ $$$$\underset{{x}\rightarrow{a}} {\mathrm{lim}}{f}\left({x}\right)=\infty\:{has}\:{meaning}. \\ $$
Commented by JDamian last updated on 02/Feb/21
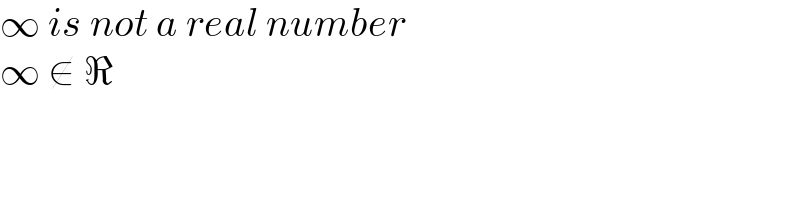
$$\infty\:{is}\:{not}\:{a}\:{real}\:{number} \\ $$$$\infty\:\notin\:\Re \\ $$
Commented by mr W last updated on 02/Feb/21

$$\infty\:{is}\:{not}\:{a}\:{number}\:{at}\:{all}! \\ $$
Commented by MJS_new last updated on 03/Feb/21
![I still believe that if f(x)=[term without x] ⇒ (d/dx)[f(x)]=0 example: f(x)=(1/r); r∈R ⇒ (d/dx)[f(x)]=0 we have the limit f′(p)=lim_(h→0) ((f(p+h)−f(p−h))/(2h)) in this case f′(p)=lim_(h→0) lim_(r→0) (((1/r)−(1/r))/(2h)) = =lim_(h→0) lim_(r→0) (0/(2h)) =0 if I′m wrong please prove](https://www.tinkutara.com/question/Q131272.png)
$$\mathrm{I}\:\mathrm{still}\:\mathrm{believe}\:\mathrm{that}\:\mathrm{if}\:{f}\left({x}\right)=\left[{term}\:{without}\:{x}\right] \\ $$$$\Rightarrow\:\frac{{d}}{{dx}}\left[{f}\left({x}\right)\right]=\mathrm{0} \\ $$$$\mathrm{example}: \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{r}};\:{r}\in\mathbb{R}\:\Rightarrow\:\frac{{d}}{{dx}}\left[{f}\left({x}\right)\right]=\mathrm{0} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{the}\:\mathrm{limit} \\ $$$${f}'\left({p}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{f}\left({p}+{h}\right)−{f}\left({p}−{h}\right)}{\mathrm{2}{h}} \\ $$$$\mathrm{in}\:\mathrm{this}\:\mathrm{case} \\ $$$${f}'\left({p}\right)=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\underset{{r}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\frac{\mathrm{1}}{{r}}−\frac{\mathrm{1}}{{r}}}{\mathrm{2}{h}}\:= \\ $$$$=\underset{{h}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\underset{{r}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{0}}{\mathrm{2}{h}}\:=\mathrm{0} \\ $$$$\mathrm{if}\:\mathrm{I}'\mathrm{m}\:\mathrm{wrong}\:\mathrm{please}\:\mathrm{prove} \\ $$
Commented by mr W last updated on 03/Feb/21

$${yes},{f}\left({x}\right)\:{musn}'{t}\:{have}\:{term}\:{with}\:{x},\:{but} \\ $$$${it}\:{must}\:{be}\:{validly}\:{defined}\:{and}\: \\ $$$${represent}\:{values}. \\ $$
Answered by prakash jain last updated on 03/Feb/21

$$\frac{{d}}{{dx}}\left(\infty\right)=\mathrm{0} \\ $$
