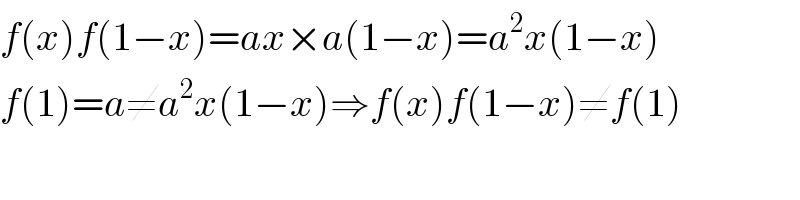f-x-f-1-x-f-1-f-x-

Question Number 4261 by 123456 last updated on 06/Jan/16

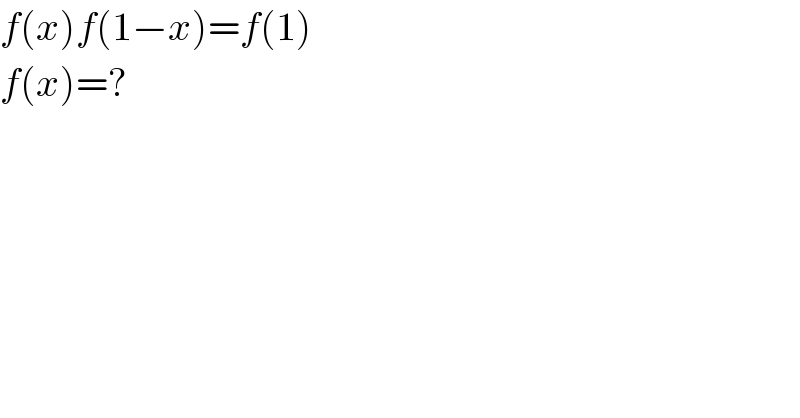
f (x) f (1 - x) = f (1)

f (x) = ?

Commented by Yozzii last updated on 06/Jan/16

f (x) = 0 f o r e x a m p l e .

f (x) f (1 - x) = f (1) = c o n s t a n t .

\Rightarrow f^{'} (x) f (1 - x) - f (x) f^{^{'}} (1 - x) = 0

\frac{f^{^{'}} (x)}{f^{^{'}} (1 - x)} = \frac{f (x)}{f (1 - x)} = r (x)

x = 1 : f (1) f (0) = f (1) \Rightarrow f (0) = 1 i f f (1) \neq 0 .

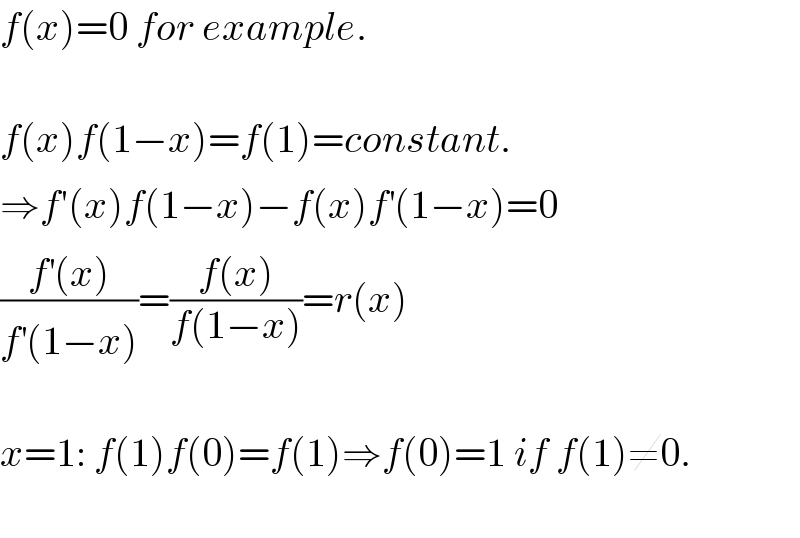
Answered by prakash jain last updated on 07/Jan/16

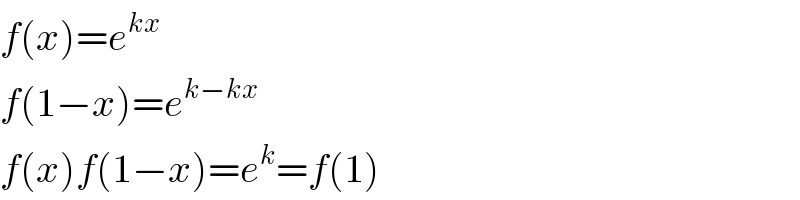
f (x) = e^{k x}

f (1 - x) = e^{k - k x}

f (x) f (1 - x) = e^{k} = f (1)

Commented by prakash jain last updated on 07/Jan/16

Thanks . Deleted f (x) + f (1 - x) part of answer .

Commented by Yozzii last updated on 07/Jan/16

f (x) f (1 - x) = a x \times a (1 - x) = a^{2} x (1 - x)

f (1) = a \neq a^{2} x (1 - x) \Rightarrow f (x) f (1 - x) \neq f (1)

Facebook Tweet Pin